Descubre qué es el sucesor de un número y amplía tus conocimientos matemáticos de manera emocionante

Las matemáticas son una disciplina fundamental para nuestra vida cotidiana y enriquecen nuestro pensamiento lógico. Una de las nociones básicas en matemáticas es el concepto de sucesor. El sucesor de un número es aquel que le sigue en orden, es decir, el siguiente número después de él.

Exploraremos a fondo qué es el sucesor de un número y cómo se puede calcular. También veremos algunos ejemplos prácticos para comprender mejor este concepto. Además, descubriremos la importancia del sucesor en operaciones matemáticas y cómo se utiliza en diversas ramas de las matemáticas, como la aritmética y el álgebra. ¡Prepárate para ampliar tus conocimientos y adentrarte en el fascinante mundo de los números!

Qué es el sucesor de un número y por qué es importante en matemáticas

En matemáticas, el concepto de sucesor de un número es fundamental para comprender y operar con números enteros. El sucesor de un número se define como el número que le sigue inmediatamente en la secuencia numérica, es decir, es el número siguiente.

Para entender mejor este concepto, necesitamos tener claro qué es un número entero. Los números enteros son aquellos que incluyen tanto los números positivos como los negativos, junto con el cero. La secuencia numérica de los enteros se extiende infinitamente en ambas direcciones: hacia los números negativos (-1, -2, -3, ...) y hacia los números positivos (1, 2, 3, ...). Entre cada par de números enteros consecutivos existe un número llamado sucesor.

El sucesor de cualquier número entero positivo es simplemente el número entero siguiente. Por ejemplo, el sucesor de 5 es 6, el sucesor de 10 es 11, y así sucesivamente. De manera inversa, si consideramos un número entero negativo, el sucesor de dicho número será el número entero positivo siguiente. Por ejemplo, el sucesor de -4 es -3, el sucesor de -10 es -9, y así sucesivamente.

La importancia del concepto de sucesor radica en su aplicación en diferentes áreas de las matemáticas. Es especialmente relevante en la aritmética y el álgebra, ya que muchas operaciones y propiedades de los números enteros se basan en el concepto de sucesor.

Aplicaciones del concepto de sucesor

1. Cálculo de términos en una sucesión: Una sucesión es una secuencia ordenada de números donde cada número se obtiene a partir del anterior mediante alguna regla o patrón. Conocer el concepto de sucesor nos permite calcular los términos siguientes en la sucesión, lo que resulta útil para resolver problemas matemáticos y plantear ecuaciones recurrentes.

2. Ordenación de números enteros: El concepto de sucesor también se utiliza para establecer un orden en los números enteros. Al conocer el sucesor de un número, podemos determinar si este es mayor o menor que otro número entero. Asimismo, podemos utilizar el método de sucesivos sucesores para ordenar una lista de números enteros de forma ascendente o descendente.

3. Operaciones aritméticas: En la aritmética, las operaciones básicas como la suma y la resta también están relacionadas con el concepto de sucesor. Al sumar dos números enteros consecutivos, el resultado será el sucesor del número más pequeño. Por ejemplo, 3 + 4 = 7, donde 7 es el sucesor de 3. De manera similar, al restar un número entero del sucesor de otro número, obtendremos el resultado de una resta sucesiva. Por ejemplo, 7 - 5 = 2, donde 2 es el sucesor de 5.

El sucesor de un número es aquel que le sigue inmediatamente en la secuencia numérica. Es un concepto clave en matemáticas, utilizado en áreas como la aritmética, el álgebra y la resolución de problemas. Comprender y operar con los sucesores de los números permite desarrollar habilidades matemáticas importantes y ampliar nuestros conocimientos en esta apasionante disciplina.

Cómo se calcula el sucesor de un número

La idea de calcular el sucesor de un número puede resultar sencilla para algunos, pero en realidad implica una serie de conceptos matemáticos que pueden enriquecer nuestra comprensión del mundo numérico. El sucesor de un número se define como aquel número que le sigue o viene después de él en una secuencia determinada.

Para calcular el sucesor de un número, simplemente se debe sumarle 1 al número dado. Es decir, si tenemos un número , su sucesor sería + 1. Esta operación es básica y se utiliza a menudo en matemáticas elementales.

El concepto de sucesor es muy importante en diferentes áreas de las matemáticas, ya que permite establecer relaciones de orden y comparación entre los números. Por ejemplo, podemos utilizar el sucesor para establecer si un número es mayor o menor que otro. Si el sucesor de un número A es igual a otro número B, entonces podemos inferir que A es menor que B.

Además, el cálculo del sucesor puede ser extendido a cualquier tipo de número, ya sea entero, decimal o incluso negativo. La suma de 1 al número siempre dará como resultado el sucesor correspondiente.

¿Cómo se aplica el concepto de sucesor en la vida cotidiana?

Aunque pueda parecer que el concepto de sucesor es algo abstracto y únicamente relacionado con las matemáticas, en realidad tiene aplicaciones prácticas en nuestra vida diaria.

Por ejemplo, cuando contamos objetos o elementos, estamos utilizando indirectamente el concepto de sucesor. Al contar, identificamos cada objeto y establecemos un orden secuencial donde cada elemento tiene un sucesor que le sigue en la secuencia. Sin el concepto de sucesor, sería difícil organizar y contar cualquier conjunto de elementos.

Además, en situaciones que involucran fechas y tiempos, también se aplica el concepto de sucesor de manera explícita. Cada día, al avanzar en el calendario, estamos calculando el sucesor del día anterior. De igual manera, cuando hablamos de los minutos o segundos en una hora, estamos aplicando el mismo concepto, ya que cada incremento de tiempo implica sumar 1 al valor previo.

El cálculo del sucesor de un número es una operación básica que nos permite comprender las relaciones de orden entre los números. Aunque puede parecer abstracto, su aplicación en la vida cotidiana es evidente y nos ayuda a organizar, contar y establecer secuencias en diferentes situaciones.

Cuál es la relación entre el sucesor de un número y los números consecutivos

El concepto de sucesor de un número está estrechamente relacionado con los números consecutivos. Para entender esta relación, primero debemos comprender qué es exactamente el sucesor de un número.

En matemáticas, el sucesor de un número entero se obtiene sumando 1 al número dado. Por ejemplo, el sucesor de 5 es 6, el sucesor de -3 es -2 y así sucesivamente. Podemos notar que el sucesor siempre sigue de manera inmediata al número original, lo que nos lleva a la noción de números consecutivos.

Los números consecutivos son aquellos que aparecen en orden sin ningún número intermedio. Si tomamos un número cualquiera y le sumamos sucesivamente el sucesor, obtendremos una secuencia de números consecutivos.

Por ejemplo, si partimos del número 3 y le sumamos el sucesor (que es 4), obtenemos 7. Si volvemos a sumar el sucesor de 7, que es 8, obtenemos 15. Esta secuencia de números: 3, 7, 15, constituye una serie de números consecutivos.

Aplicaciones prácticas de la noción de sucesor y números consecutivos

La comprensión de la relación entre el sucesor de un número y los números consecutivos tiene aplicaciones muy útiles en diversos ámbitos de las ciencias y las matemáticas.

• Aritmética: El estudio de los números consecutivos y el sucesor de un número son fundamentales en el campo de la aritmética. Estos conceptos nos permiten comprender la estructura de las secuencias numéricas y realizar operaciones matemáticas básicas.
• Programación: En programación, la noción de sucesor y números consecutivos es utilizada frecuentemente. Por ejemplo, al implementar un bucle que recorra una secuencia de números o al generar una serie de datos ordenados.
• Ciencias naturales: En disciplinas como la física o la biología, la relación entre el sucesor de un número y los números consecutivos también puede ser relevante. Por ejemplo, al estudiar cambios temporales o secuenciales en fenómenos naturales o en procesos biológicos.

El sucesor de un número se refiere al número que sigue inmediatamente a otro al sumarle 1. Los números consecutivos son aquellos que aparecen en orden sin ningún número intermedio. La comprensión de esta relación es esencial para entender diversos conceptos matemáticos y tiene aplicaciones prácticas en áreas como la aritmética, la programación y las ciencias naturales.

Cómo podemos usar el concepto de sucesor para entender mejor las secuencias numéricas

Las secuencias numéricas son una parte fundamental de las matemáticas, ya que nos permiten entender el orden y la estructura de los números. Para comprender mejor las secuencias numéricas, es importante entender qué es un sucesor.

El sucesor de un número es aquel que le sigue inmediatamente en una secuencia numérica. Por ejemplo, el sucesor del número 5 en la secuencia natural sería el número 6. En otras palabras, el sucesor de un número es aquel que se obtiene al sumarle una unidad.

El concepto de sucesor es especialmente útil para trabajar con secuencias numéricas, ya que nos permite generar fácilmente la secuencia siguiente a partir de cualquier número dado. Por ejemplo, si queremos encontrar los primeros cinco sucesores de 10, simplemente tenemos que sumarle una unidad al número inicial: 11, 12, 13, 14, 15.

Las secuencias numéricas pueden tener diferentes patrones y reglas que gobiernan su formación. Algunas secuencias pueden aumentar de manera constante (secuencia ascendente), mientras que otras pueden disminuir en cada término (secuencia descendente). El sucesor nos ayuda a entender cómo se generan estas secuencias.

Además, el concepto de sucesor también se utiliza en otros campos de las matemáticas, como el álgebra y la teoría de conjuntos. En álgebra, por ejemplo, se utiliza el término "sucesión" para referirse a un conjunto ordenado de números en el que cada uno está relacionado con el anterior mediante una regla.

El sucesor de un número nos permite entender cómo se generan las secuencias numéricas y nos ayuda a avanzar en la comprensión de conceptos matemáticos más complejos. Es una herramienta fundamental para ampliar nuestros conocimientos y explorar nuevas áreas de las matemáticas.

Cuáles son algunos ejemplos prácticos del uso del sucesor de un número

El sucesor de un número es una herramienta fundamental en las matemáticas, y su utilidad no se limita únicamente a cálculos abstractos. En la vida cotidiana, existen numerosos ejemplos prácticos en los que podemos aplicar el concepto del sucesor para resolver problemas o tomar decisiones.

1. Conteo y numeración

Uno de los usos más comunes del sucesor de un número es en el conteo y la numeración. Desde temprana edad, aprendemos a contar y asignar números sucesivos a diferentes objetos o elementos. Por ejemplo, al contar los juguetes en una habitación, podemos utilizar el sucesor para asignar un número a cada uno de ellos: 1, 2, 3, 4, y así sucesivamente.

2. Calendario y fechas

En el calendario y al trabajar con fechas, también recurrimos al sucesor de un número. Cada día tiene un sucesor, es decir, el siguiente día en la secuencia. Esto nos permite determinar fácilmente qué día vendrá después de otro, o calcular la diferencia entre dos fechas. Por ejemplo, si hoy es jueves, el sucesor será viernes; y si quiero saber cuántos días faltan para mi cumpleaños, puedo restar el número actual del día al sucesor de la fecha de mi cumpleaños.

3. Secuencias y patrones

Cuando trabajamos con secuencias numéricas o patrones, el sucesor de un número nos ayuda a encontrar la relación entre los elementos y predecir el siguiente término. Por ejemplo, en la secuencia 2, 4, 6, 8, el sucesor de cada número es el que le sigue en la secuencia, lo que nos permite identificar fácilmente el patrón: sumar 2 en cada paso. Esta habilidad es especialmente útil en campos como la programación, donde se utilizan algoritmos basados en secuencias numéricas.

4. Operaciones aritméticas

En operaciones aritméticas básicas, como la suma y la resta, el uso del sucesor de un número simplifica los cálculos. Por ejemplo, si tenemos la operación 7 + 1, podemos utilizar el sucesor de 7 (que es 8) para obtener directamente el resultado sin necesidad de contar o sumar individualmente cada número.

5. Progresiones numéricas

En las progresiones numéricas, el concepto de sucesor es esencial. Las progresiones son secuencias de números en las que cada término se obtiene sumando o restando una constante al término anterior. El sucesor de un número es la base para construir estas progresiones y analizarlas matemáticamente.

6. Programación y algoritmos

En el campo de la programación y los algoritmos, el concepto del sucesor de un número es fundamental. En muchos lenguajes de programación, se utilizan ciclos "for" o "while" para iterar una determinada cantidad de veces. En estos casos, el sucesor de un número se utiliza para controlar el número de iteraciones y asegurar que la lógica del programa se repita el número de veces necesario.

¡Estos son solo algunos ejemplos prácticos donde el sucesor de un número juega un papel clave! Su uso es fundamental en matemáticas, pero también tiene aplicaciones prácticas en diversos aspectos de nuestra vida diaria. Ahora que conoces su importancia, podrás ampliar tus conocimientos matemáticos y utilizar esta herramienta para resolver problemas y tomar decisiones de una manera emocionante.

¿Existen límites para los sucesores de los números? Explora las posibilidades infinitas.

Los sucesores de los números son una herramienta fundamental en matemáticas que nos permite avanzar a través de la secuencia numérica de manera sistemática. Pero, ¿alguna vez te has preguntado si existen límites para los sucesores de los números? ¡La respuesta es emocionante!

En términos simples, el sucesor de un número es simplemente el siguiente número en la secuencia. Por ejemplo, el sucesor de 8 es 9, y el sucesor de -3 es -2. Pero, ¿hay algún límite para estos sucesores?

La respuesta es no, no hay límites para los sucesores de los números. La razón detrás de esto radica en el concepto mismo de infinito en las matemáticas. Como sabemos, el conjunto de los números naturales (1, 2, 3, ...) es infinito, lo que significa que no tiene un final definido.

Siempre podemos encontrar el sucesor de cualquier número dado. Si tomamos cualquier número natural y le sumamos 1, obtendremos su sucesor. Y si tomamos cualquier número entero negativo y le sumamos 1, también obtendremos su sucesor en forma de un número entero más cercano al cero.

La belleza de la infinitud

Esta falta de límites en los sucesores de los números nos muestra la belleza de la infinitud en las matemáticas. Nos permite explorar las posibilidades infinitas de la secuencia numérica, sin importar cuán grande o pequeño sea el número inicial.

Por ejemplo, si comenzamos con el número 1 y vamos encontrando sus sucesores de forma sistemática, obtendremos una secuencia infinita: 1, 2, 3, 4, 5, 6, ... ¡y así sucesivamente! No importa cuántos números agreguemos, siempre hay un número más grande esperando a ser descubierto.

Del mismo modo, si comenzamos con un número negativo como -100 y encontramos los sucesores sumando 1, obtendremos una secuencia infinita en la dirección opuesta: -100, -99, -98, -97, ... ¡y así sucesivamente! Aquí también podemos ver que no hay límites para los sucesores de los números negativos.

El papel de los sucesores en otros campos de las matemáticas

Aunque pensar en los sucesores de los números puede parecer una idea simple y elemental, estos conceptos tienen un papel crucial en otras ramas de las matemáticas, como el cálculo y la teoría de conjuntos.

En el cálculo, por ejemplo, el concepto de límite se basa en el uso de sucesiones. Una sucesión es simplemente una lista ordenada de números que sigue una regla específica. El límite de una sucesión es el valor hacia el cual tienden los términos de la sucesión cuando el número de términos se acerca al infinito.

• Los sucesores de los números nos permiten avanzar de manera infinita en la secuencia numérica.
• No hay límites para los sucesores de los números, ya que el conjunto de los números naturales es infinito.
• La belleza de la infinitud se revela a través de las posibilidades infinitas de los sucesores de los números.
• Los sucesores juegan un papel crucial en otras áreas de las matemáticas, como el cálculo y la teoría de conjuntos.

Los sucesores de los números son una herramienta fascinante que nos permite explorar la secuencia numérica de manera sistemática e infinita. No hay límites para los sucesores, lo que significa que siempre podemos encontrar un número más grande o más pequeño dependiendo del punto de partida. ¡Así que sigue adelante y descubre las maravillas que los sucesores pueden ofrecer!

Cómo podemos aplicar el concepto de sucesor en otras áreas de las matemáticas, como el álgebra o la geometría

El concepto de sucesor es fundamental en el estudio de las matemáticas. Si bien es comúnmente utilizado en el contexto de los números naturales, donde cada número tiene un sucesor único, este concepto también puede ser aplicado en otras áreas de las matemáticas, como el álgebra o la geometría.

En el álgebra, el concepto de sucesor se utiliza para hablar de secuencias y sucesiones. Una sucesión es una lista ordenada de números en la que cada número es el sucesor del anterior. Por ejemplo, la sucesión 1, 2, 3, 4, ... muestra cómo cada número es el sucesor del número anterior. Estas sucesiones pueden ser utilizadas para modelar situaciones del mundo real, como el crecimiento de poblaciones, la evolución de precios o incluso el valor de una inversión a lo largo del tiempo.

En la geometría, el concepto de sucesor se aplica en la construcción de figuras geométricas o en la demostración de teoremas. Por ejemplo, cuando queremos construir una línea recta, podemos comenzar con un punto y utilizar el concepto de sucesor para agregar puntos adicionales y formar la línea completa. De manera similar, en la demostración de un teorema, podemos utilizar el concepto de sucesor para ir paso a paso mostrando cómo se llega al resultado deseado.

Cómo podemos representar el concepto de sucesor en términos algebraicos o geométricos

En términos algebraicos, el concepto de sucesor puede ser representado a través de operaciones matemáticas. Por ejemplo, si tenemos un número n, el sucesor de ese número puede ser representado como n + 1. De esta manera, podemos generar secuencias o sucesiones utilizando operaciones algebraicas.

En cuanto a la geometría, el concepto de sucesor puede ser representado a través de la construcción de figuras geométricas o el uso de puntos adicionales. Por ejemplo, si queremos construir una línea recta, podemos comenzar con un punto y utilizar el concepto de sucesor para agregar puntos adicionales y formar la línea completa.

Es importante destacar que el concepto de sucesor no se limita únicamente al álgebra y la geometría. Podemos encontrar aplicaciones del concepto de sucesor en muchas otras áreas de las matemáticas, como el cálculo, la teoría de conjuntos o la teoría de grafos. El concepto de sucesor nos permite estudiar y comprender el orden y la relación entre los elementos de un conjunto o secuencia.

El concepto de sucesor es una herramienta fundamental en las matemáticas que nos permite estudiar y comprender la relación y el orden entre los elementos de un conjunto o secuencia. Además de su aplicación en el estudio de los números naturales, el concepto de sucesor también puede ser utilizado en el álgebra, la geometría y otras ramas de las matemáticas. Entender y aplicar este concepto nos permite ampliar nuestros conocimientos matemáticos y explorar nuevas áreas de estudio de manera emocionante.

Cuál es la importancia del sucesor de un número en el desarrollo de habilidades de razonamiento lógico

El sucesor de un número es un concepto fundamental en el campo de las matemáticas y desempeña un papel crucial en el desarrollo de habilidades de razonamiento lógico. Comprender qué es el sucesor de un número puede abrir un mundo de posibilidades para los estudiantes, ayudándolos a adquirir una comprensión más profunda de la estructura numérica y fortaleciendo su capacidad para resolver problemas.

En términos sencillos, el sucesor de un número es simplemente el número que le sigue en orden. Por ejemplo, si tenemos el número 5, su sucesor sería el número 6. Parece una idea simple, pero en realidad tiene implicaciones significativas en las matemáticas.

Al comprender el concepto de sucesor, los estudiantes pueden comenzar a explorar una variedad de temas matemáticos más avanzados, como secuencias numéricas, sistemas de conteo y operaciones aritméticas básicas. El sucesor también proporciona una base sólida para entender conceptos posteriores como números pares e impares, sumas y restas, multiplicación y división.

Beneficios de comprender el sucesor de un número

• Fortalecimiento del razonamiento lógico: Al trabajar con sucesores, los estudiantes aprenden a percibir relaciones y patrones entre números, lo que estimula el pensamiento lógico y la capacidad de resolución de problemas.
• Desarrollo de habilidades de cálculo: Al reconocer los sucesores de un número, se facilita la adquisición de habilidades matemáticas básicas como sumar o contar.
• Aplicación en situaciones cotidianas: El entendimiento del sucesor de un número es útil en diversas situaciones de la vida diaria, como contar objetos, organizar secuencias o resolver problemas prácticos.
• Precursor de conceptos más avanzados: El sucesor es un punto de partida esencial para comprender otros conceptos numéricos, como números pares e impares, y avanzar hacia áreas de las matemáticas más complejas.

El sucesor de un número es un pilar fundamental en el desarrollo de habilidades matemáticas y razonamiento lógico. Comprender esta noción básica puede abrir las puertas a un mundo de conocimiento numérico y ayudar a los estudiantes a desarrollar una sólida base de habilidades matemáticas que les servirá a lo largo de sus estudios y en su vida cotidiana.

Cómo podemos enseñar a los niños sobre el concepto de sucesor de una manera divertida y accesible

Enseñar a los niños sobre el concepto de sucesor puede ser un desafío, especialmente si quieren aprender de una manera divertida y accesible. Afortunadamente, existen muchas actividades emocionantes que podemos utilizar para ayudar a los niños a comprender este importante concepto matemático.

Juegos interactivos

Una excelente manera de enseñar el concepto de sucesor es a través de juegos interactivos. Estos juegos permiten a los niños aprender mientras se divierten, lo que hace que el proceso sea mucho más emocionante y memorable.

• Uno de los juegos populares es "La carrera del sucesor". En este juego, los niños deben avanzar en un tablero numerado y decir el número que sigue al número en el que están parados. Esto les permite practicar tanto la secuencia numérica como el concepto de sucesor.
• Otro juego divertido es "Encuentra al sucesor". En este juego, se muestra a los niños una serie de números y deben identificar el número que sigue en la secuencia. Puedes hacer esto utilizando tarjetas con números o incluso utilizando una aplicación en línea.

Aprender a través de manipulativos

Los manipulativos son objetos físicos que los niños pueden tocar y mover para ayudar a comprender conceptos abstractos. Al utilizar manipulativos para enseñar el concepto de sucesor, los niños pueden ver y experimentar cómo cada número sigue al anterior.

Por ejemplo, puedes utilizar bloques de construcción para representar cada número. Pide a los niños que coloquen los bloques en orden y señalen el sucesor de cada número. Esto les permite visualizar la secuencia numérica y comprender cómo cada número está relacionado con el siguiente.

Actividades prácticas

Además de los juegos y manipulativos, las actividades prácticas también pueden ser una forma efectiva de enseñar el concepto de sucesor. Estas actividades permiten a los niños aplicar lo que han aprendido en situaciones cotidianas.

Por ejemplo, puedes jugar a "Simon dice". Pide a los niños que realicen una acción (como saltar o dar un paso adelante) cada vez que menciones el sucesor de un número. Esto les ayuda a asociar el concepto a acciones concretas y les permite practicar tanto la secuencia numérica como el concepto de sucesor de una manera divertida.

También puedes utilizar problemas matemáticos donde los niños tengan que encontrar el sucesor de un número para resolverlos. Estos problemas pueden presentarse en forma de acertijos o rompecabezas, lo que añade un elemento de diversión y desafío al proceso de aprendizaje.

Enseñar a los niños sobre el concepto de sucesor puede ser emocionante y accesible si utilizamos juegos interactivos, manipulativos y actividades prácticas. Estas estrategias ayudan a los niños a comprender y aplicar este importante concepto matemático de una manera divertida y significativa.

Existe alguna aplicación real o práctica del concepto de sucesor en el mundo cotidiano más allá de las matemáticas

El concepto de sucesor es una noción fundamental dentro de las matemáticas, especialmente en el campo de la aritmética. Pero, ¿existe alguna aplicación real o práctica de este concepto en el mundo cotidiano más allá de la teoría matemática?

A primera vista, podría parecer que el concepto de sucesor no tiene mucha relevancia fuera del ámbito académico. Sin embargo, si consideramos cómo se puede interpretar el sucesor en diferentes contextos, podemos descubrir que este concepto tiene aplicaciones interesantes en diversas situaciones de la vida diaria.

Aplicaciones en secuencias y patrones

Una de las formas más evidentes en las que podemos encontrar el concepto de sucesor en el mundo real es en las secuencias y patrones. Muchas veces, en nuestro entorno, nos encontramos con series de eventos, objetos o acciones que siguen un orden lógico y se repiten consecutivamente. En estos casos, el sucesor se refiere al siguiente elemento de la serie.

Por ejemplo, imaginemos una secuencia de colores en un semáforo: rojo, amarillo, verde. En este caso, el sucesor de rojo es amarillo, y el sucesor de amarillo es verde. Esta secuencia sigue un patrón lógico y se repite continuamente siguiendo esta estructura. La comprensión del concepto de sucesor nos permite entender cómo se desarrolla y organiza esta secuencia.

Representación de estados o etapas

Otra forma en la que podemos aplicar el concepto de sucesor en el mundo cotidiano es en la representación de estados o etapas dentro de un proceso. Muchas veces, en diferentes áreas como la tecnología, la industria o la investigación científica, se trabaja con procesos que constan de diferentes fases o etapas.

En estos casos, cada etapa o fase puede considerarse como un sucesor del anterior. Por ejemplo, en el desarrollo de software, podemos dividir el proceso en varias etapas como diseño, implementación y pruebas. Cada una de estas etapas representa un paso adelante en el progreso del proyecto y puede considerarse como el sucesor de la etapa anterior.

Modelado de situaciones y eventos

El concepto de sucesor también puede ser aplicado en el modelado de situaciones y eventos en diferentes contextos. Por ejemplo, en la planificación de rutas de transporte, es necesario tener en cuenta diferentes paradas o puntos de interés a lo largo del trayecto.

Cada uno de estos puntos de interés puede considerarse como un sucesor del anterior, ya que representan ubicaciones consecutivas en el recorrido. El concepto de sucesor nos permite organizar y estructurar eficientemente la secuencia de paradas en el orden apropiado.

Aunque el concepto de sucesor es fundamentalmente matemático, tiene aplicaciones interesantes en el mundo real más allá de las matemáticas. En contextos como secuencias y patrones, representación de estados o etapas, y modelado de situaciones y eventos, el concepto de sucesor nos ayuda a comprender mejor y organizar diferentes aspectos de la vida cotidiana.

El sucesor de un número es el número que le sigue inmediatamente en la secuencia numérica.

Para encontrar el sucesor de un número, simplemente le sumas 1 al número dado.

No, cada número tiene un único sucesor en la secuencia numérica.

El sucesor del cero es el número uno.

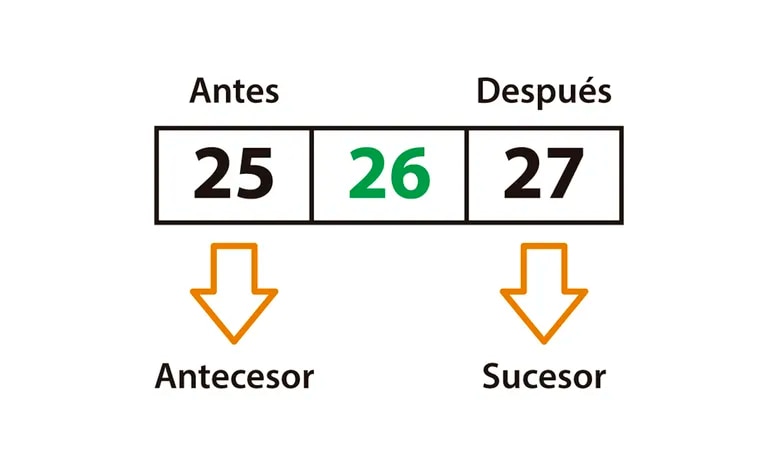
El sucesor de un número es el número que le sigue, mientras que el antecesor de un número es el número que le precede. Son conceptos opuestos pero complementarios.