Fácil y rápido: Aprende cómo sacar la mediatriz de un triángulo y resuelve tus dudas matemáticas

Las matemáticas pueden resultar difíciles para algunos, especialmente cuando se trata de geometría y figuras geométricas. Uno de los conceptos que puede causar confusiones es la mediatriz de un triángulo. Sin embargo, entender qué es y cómo sacarla puede ser más fácil de lo que imaginas.

Te explicaremos qué es la mediatriz de un triángulo, cómo encontrarla a partir de sus puntos medios y cuál es su importancia en la geometría. Además, te mostraremos paso a paso cómo calcularla en diferentes situaciones, para que puedas resolver cualquier duda matemática relacionada con este tema.

Qué es la mediatriz de un triángulo y para qué sirve

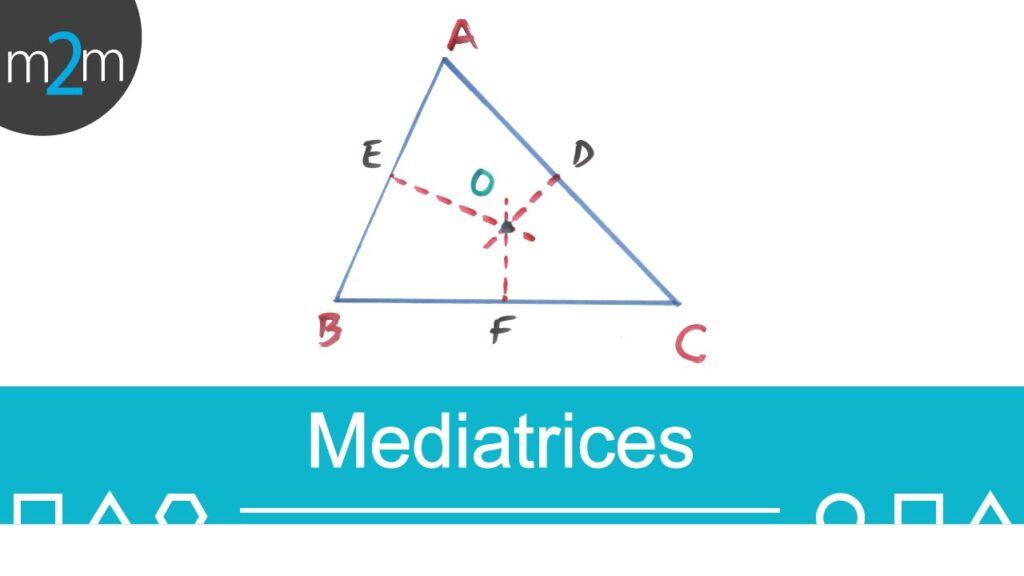
La mediatriz de un triángulo es una línea recta que pasa por el punto medio de un lado y es perpendicular a ese lado. Cada triángulo tiene tres mediatrices, una para cada lado. La mediatriz divide al triángulo en dos partes iguales, tanto en longitud como en área.

La mediatriz de un triángulo no solo es un concepto teórico, sino que también tiene aplicaciones prácticas en resolución de problemas matemáticos y construcción geométrica. En geometría, la mediatriz puede utilizarse para encontrar el centro del círculo circunscrito al triángulo, ya que las tres mediatrices convergen en un único punto llamado circumcentro. Además, la mediatriz es útil para construir triángulos equiláteros y resolver problemas relacionados con las propiedades de los triángulos isósceles.

Cómo sacar la mediatriz de un triángulo

Para sacar la mediatriz de un triángulo, necesitas conocer el punto medio de uno de los lados del triángulo. A partir de ese punto medio, debes trazar una línea perpendicular al lado correspondiente.

Una forma sencilla de encontrar el punto medio de un lado del triángulo es ubicar los dos extremos del lado y calcular el promedio de sus coordenadas. Por ejemplo, si tienes un lado con los puntos A(x1, y1) y B(x2, y2), el punto medio M será (xm, ym), donde:

xm = (x1 + x2) / 2
ym = (y1 + y2) / 2

Una vez que tienes el punto medio M, traza una línea perpendicular a ese lado utilizando una regla y un compás. Coloca la punta seca del compás en el punto medio M y ajusta la longitud del compás para que alcance cualquier punto del lado correspondiente. Traza dos arcos desde M hasta los dos extremos del lado, creando dos intersecciones con el lado.

Por último, une las dos intersecciones de los arcos con una línea recta. Esta línea recta será la mediatriz del triángulo, ya que pasa por el punto medio del lado y es perpendicular a él. Si realizas este proceso para cada lado del triángulo, obtendrás las tres mediatrices que se intersectan en un punto llamado circumcentro.

Resuelve tus dudas matemáticas sobre la mediatriz

La mediatriz puede resultar confusa al principio, pero con la práctica y la comprensión adecuada, puedes dominarla rápidamente. Si tienes alguna pregunta o dificultad al sacar la mediatriz de un triángulo, no dudes en consultar a tu profesor de matemáticas o buscar recursos adicionales en línea.

Además, existen numerosos videos y tutoriales en línea que pueden ayudarte a visualizar el concepto de la mediatriz y su aplicación en la resolución de problemas matemáticos. Aprovecha estos recursos para fortalecer tus habilidades matemáticas y superar cualquier obstáculo que encuentres en tu camino hacia el dominio de la mediatriz.

Recuerda que la práctica y la perseverancia son clave para comprender y aplicar conceptos matemáticos. No te desanimes si al principio encuentras dificultades, con el tiempo podrás resolver cualquier duda sobre la mediatriz de un triángulo y utilizarla eficazmente en tus estudios y en la resolución de problemas geométricos.

Cuál es el proceso paso a paso para sacar la mediatriz de un triángulo

La mediatriz de un triángulo es una línea perpendicular que pasa por el punto medio de cada lado del triángulo. En otras palabras, es la línea que divide un lado del triángulo en dos partes iguales y forma ángulos rectos con ese lado.

Para sacar la mediatriz de un triángulo, se siguen varios pasos que son fáciles de entender y aplicar. A continuación, te explicaré el proceso paso a paso:

Paso 1: Dibuja un triángulo

Lo primero que debes hacer es dibujar un triángulo en un papel. Puedes utilizar una regla y un lápiz para garantizar que los lados y ángulos del triángulo sean precisos. Recuerda que un triángulo tiene tres lados y tres ángulos.

Paso 2: Encuentra los puntos medios de cada lado

Ahora, necesitas encontrar los puntos medios de cada lado del triángulo. El punto medio de un lado es el punto que divide ese lado exactamente en dos partes iguales. Utiliza tu regla para medir cada lado del triángulo y marca el punto medio con un pequeño punto.

Paso 3: Traza líneas perpendiculares desde los puntos medios

A partir de cada punto medio marcado en el paso anterior, traza una línea perpendicular al lado correspondiente del triángulo. Para hacer esto, coloca la punta de tu compás en el punto medio y traza un arco que intersecte ambos extremos del lado del triángulo. Haz lo mismo para los otros dos puntos medios.

Paso 4: Encuentra el punto de intersección

Las líneas perpendiculares que trazaste en el paso anterior se cortarán en un punto. Este punto es el centro del círculo que circunscribe el triángulo y donde se encuentra la mediatriz. Utiliza tu regla para dibujar una línea recta que pase por este punto de intersección y atraviese el triángulo. Esta línea es la mediatriz.

Ahora que has aprendido cómo sacar la mediatriz de un triángulo, puedes resolver tus dudas matemáticas relacionadas con este tema. Recuerda practicar estos pasos con diferentes triángulos para afianzar tu comprensión. ¡No temas a las matemáticas, pueden ser más fáciles de lo que parecen!

Cómo se calcula la ecuación de la mediatriz a partir de los puntos del triángulo

La mediatriz de un triángulo es una línea que pasa por el punto medio de uno de sus lados y es perpendicular a este lado. Es una herramienta muy útil en geometría para determinar propiedades importantes del triángulo. Afortunadamente, el cálculo de la ecuación de la mediatriz es bastante sencillo.

Para calcular la ecuación de la mediatriz, necesitamos tener los puntos de dos vértices del triángulo. En este caso, llamaremos a estos puntos A(x1, y1) y B(x2, y2). Además, supongamos que queremos determinar la mediatriz del segmento AB.

El primer paso para calcular la ecuación de la mediatriz es encontrar el punto medio del segmento AB. Esto se puede hacer utilizando la fórmula:

xm = (x1 + x2)/2
ym = (y1 + y2)/2

Donde xm y ym representan las coordenadas del punto medio. Ahora que tenemos las coordenadas del punto medio M(xm, ym), podemos pasar al siguiente paso.

El siguiente paso es determinar la pendiente de la mediatriz, que es simplemente la pendiente negativa del segmento AB. La fórmula para calcular la pendiente m entre dos puntos P(x1, y1) y Q(x2, y2) es:

m = (y2 - y1)/(x2 - x1)

Por lo tanto, la pendiente de la mediatriz es:

m_perpendicular = -1/m

Finalmente, tenemos la pendiente de la mediatriz y las coordenadas del punto medio M(xm, ym). Ahora podemos utilizar la ecuación de la recta para determinar la ecuación de la mediatriz.

La ecuación de la mediatriz en forma punto-pendiente es:

y - ym = m_perpendicular * (x - xm)

Donde y y x representan coordenadas genéricas en la recta y ym y xm representan las coordenadas del punto medio. Esta ecuación se puede manipular para obtener la forma ordenada-pendiente si es necesario.

El cálculo de la ecuación de la mediatriz a partir de los puntos del triángulo implica encontrar el punto medio del segmento dado y determinar su pendiente. Luego, utilizando la fórmula de la recta en forma punto-pendiente, podemos obtener fácilmente la ecuación de la mediatriz.

Esperamos que esta explicación te haya ayudado a comprender cómo sacar la mediatriz de un triángulo. Recuerda practicar con ejemplos adicionales para mejorar tu comprensión. ¡No dudes en consultar cualquier duda matemática que tengas!

Cuáles son las propiedades y características importantes de la mediatriz

La mediatriz es una línea perpendicular que se traza desde el punto medio de un segmento hasta su extremo opuesto. En el caso de los triángulos, podemos trazar tres mediatrices, una para cada lado del triángulo.

Existen varias propiedades y características importantes de la mediatriz en un triángulo:

1. Pasa por el punto medio

Una de las principales propiedades de la mediatriz es que pasa por el punto medio del lado al que pertenece. Esto significa que divide al lado en dos segmentos iguales, tanto en longitud como en posición.

2. Es perpendicular al lado correspondiente

La mediatriz es siempre perpendicular al lado al que pertenece. Esto significa que forma un ángulo recto (90 grados) con ese lado específico del triángulo.

3. Intersecta a otras mediatrices

Las mediatrices de los lados de un triángulo no son paralelas entre sí, a menos que el triángulo sea equilátero. Las mediatrices de dos lados distintos del triángulo siempre se intersectan en un punto llamado circuncentro. Este punto es equidistante a los tres vértices del triángulo.

4. Es única para cada lado

Cabe destacar que en un triángulo, cada lado tiene una única mediatriz correspondiente. Estas mediatrices son diferentes a las alturas y bisectrices del triángulo.

La mediatriz es una línea perpendicular que pasa por el punto medio de cada lado de un triángulo. Tiene la propiedad de ser siempre perpendicular al lado correspondiente y se intersecta con las mediatrices de los otros lados en el circuncentro del triángulo.

Entender las propiedades y características de la mediatriz es fundamental para resolver problemas matemáticos relacionados con triángulos, como determinar puntos equidistantes o encontrar la circunferencia circunscrita de un triángulo.

En qué casos la mediatriz puede ser útil en problemas matemáticos

La mediatriz de un triángulo es una línea perpendicular que pasa por el punto medio de cada lado del triángulo. Esta propiedad geométrica juega un papel importante en la resolución de diversos problemas matemáticos y es especialmente útil cuando se trabaja con triángulos.

Una de las aplicaciones más comunes de la mediatriz es encontrar el centro circunferencia de un triángulo, también conocido como circuncentro. El centro circunferencia es el punto donde se intersectan las tres mediatrices de un triángulo. Además, la distancia entre el centro circunferencia y cualquiera de los vértices del triángulo es igual, lo cual es una propiedad importante a tener en cuenta al trabajar con figuras circulares.

Otra aplicación práctica de la mediatriz es en la construcción de triángulos congruentes. Dado que la mediatriz divide cada lado del triángulo en dos segmentos iguales, podemos utilizar esta propiedad para construir triángulos que tengan lados iguales o congruentes.

Además, la mediatriz también se utiliza en la solución de problemas relacionados con ángulos en triángulos. Por ejemplo, si conocemos la longitud de los lados de un triángulo y queremos encontrar el valor de uno de los ángulos, podemos utilizar la mediatriz para determinar la altura correspondiente a ese lado y luego utilizar trigonometría para calcular el ángulo deseado.

La mediatriz de un triángulo tiene múltiples aplicaciones en la resolución de problemas matemáticos. Desde la construcción de triángulos congruentes hasta la determinación de ángulos, esta propiedad geométrica nos brinda herramientas para resolver diversos tipos de problemas y aumentar nuestra comprensión de las figuras geométricas.

Cuál es la relación entre la mediatriz y otros elementos del triángulo, como la altura o la bisectriz

La mediatriz es una línea que se traza desde el punto medio de un lado de un triángulo hasta el vértice opuesto. Esta línea tiene propiedades únicas y está relacionada con otros elementos del triángulo, como la altura y la bisectriz.

En primer lugar, la mediatriz y la altura comparten una característica fundamental: ambas son perpendiculares a un lado del triángulo. Sin embargo, mientras que la altura se dibuja desde un vértice del triángulo hasta el lado opuesto, la mediatriz se traza desde el punto medio del lado hasta el vértice opuesto. Esto significa que la mediatriz y la altura son líneas diferentes, pero ambas son perpendiculares al mismo lado.

En cuanto a la relación con la bisectriz, la mediatriz y la bisectriz también pueden ser perpendiculares en ciertos casos. La bisectriz de un triángulo es una línea que divide un ángulo en dos partes iguales, mientras que la mediatriz divide un lado en dos partes iguales. Si un triángulo es equilátero, es decir, todos sus lados y ángulos son iguales, la bisectriz y la mediatriz pueden coincidir y ser perpendiculares entre sí. Sin embargo, en triángulos escalenos o isósceles, la bisectriz y la mediatriz normalmente no son la misma línea y no son perpendiculares.

Cómo trazar la mediatriz de un triángulo

1. Identifica uno de los lados del triángulo del que deseas trazar la mediatriz.
2. Encuentra el punto medio de ese lado. Esto se puede hacer dividiendo la longitud del lado por la mitad.
3. Traza una línea recta desde el punto medio hasta el vértice opuesto del triángulo. Esta será la mediatriz.

Es importante tener en cuenta que la mediatriz siempre pasa a través del punto medio de un lado y es perpendicular a ese lado. También, puede ser útil recordar que las tres mediatrices de un triángulo siempre se intersectan en un mismo punto llamado circuncentro.

Usos y aplicaciones de la mediatriz

La mediatriz tiene varias aplicaciones y usos en matemáticas y geometría. Algunos de ellos incluyen:

• Encontrar el centroide de un triángulo: El centroide de un triángulo es el punto donde las tres medianas del triángulo se intersectan. Una mediana es una línea dibujada desde un vértice hasta el punto medio del lado opuesto. La mediatriz juega un papel importante en el cálculo del centroide de un triángulo debido a sus propiedades perpendiculares.
• Resolver problemas de construcción geométrica: La mediatriz se puede utilizar para construir triángulos y otros polígonos mediante regla y compás. La habilidad de trazar la mediatriz con precisión es fundamental para realizar estas construcciones geométricas con exactitud.
• Demostrar teoremas geométricos: La mediatriz es una herramienta útil para demostrar teoremas geométricos y desarrollar pruebas. Su relación con otros elementos del triángulo proporciona una base sólida para establecer conclusiones y razonamientos en geometría.

La mediatriz es una línea importante en un triángulo que se traza desde el punto medio de un lado hasta el vértice opuesto. Tiene propiedades perpendiculares y está relacionada con otros elementos del triángulo como la altura y la bisectriz. Además de su uso en construcción geométrica y demostración de teoremas, la mediatriz también permite calcular el centroide de un triángulo.

¿Es posible que haya más de una mediatriz en un triángulo? Explica.

Antes de responder a esta pregunta, es importante entender qué es una mediatriz en un triángulo. En geometría, la mediatriz de un segmento es una línea que lo divide en dos partes iguales, y pasa por su punto medio. Pero, ¿qué sucede cuando hablamos de mediatrices en el contexto de un triángulo?

La respuesta es sí, es posible que haya más de una mediatriz en un triángulo. En realidad, para cada lado del triángulo existe una mediatriz correspondiente. Esto se debe a que cada lado tiene su propio punto medio, y cada uno de estos puntos medios está ubicado en una posición única en relación con los otros dos.

Si trazamos las tres mediatrices en un triángulo, nos encontraremos con algo interesante: ¡se van a intersecar en un solo punto! Esta propiedad se conoce como "circuncentro" y es el centro de la circunferencia circunscrita al triángulo.

Ahora bien, ¿cómo podemos encontrar la mediatriz de un triángulo?

Para trazar la mediatriz de un lado de un triángulo, necesitamos seguir algunos pasos sencillos. Primero, identificamos el punto medio del segmento correspondiente a ese lado. Luego, trazamos una línea recta perpendicular al lado desde ese punto medio.

Para visualizar mejor este proceso, podemos usar una construcción geométrica conocida como compás y regla. Ponemos la punta seca del compás en el punto medio y abrimos el compás a una distancia mayor que la mitad de la longitud del lado. Luego, trazamos un arco que intersecta el lado en ambos extremos. Repetimos el proceso para los otros dos lados del triángulo.

Ahora que sabemos cómo encontrar las mediatrices de un triángulo, podemos utilizar este conocimiento para resolver diversos problemas matemáticos. Por ejemplo, si nos piden hallar el circumcentro de un triángulo, simplemente trazamos las mediatrices y encontramos el punto de intersección. Este punto será el centro de la circunferencia circunscrita al triángulo.

Las mediatrices son líneas perpendiculares a los lados de un triángulo y pasan por sus puntos medios. Cada lado tiene su propia mediatriz correspondiente, y todas ellas se intersectan en el circumcentro del triángulo. Son una herramienta útil para resolver problemas de geometría y explorar propiedades relacionadas con el triángulo.

Cómo puedo demostrar geométricamente que un segmento es la mediatriz de otro en un triángulo

La mediatriz de un triángulo es una línea recta que divide a otro segmento en dos partes iguales. Para demostrar geométricamente que un segmento determinado es la mediatriz de otro en un triángulo, podemos seguir los siguientes pasos:

Paso 1: Dibuja el triángulo

Comienza dibujando un triángulo en la superficie en la que estés trabajando. Asegúrate de que las medidas y ángulos del triángulo estén definidos claramente.

Paso 2: Marca los puntos medios

Localiza los puntos medios de dos de los lados del triángulo. Esto se hace dividiendo cada lado en dos partes iguales y marcando esos puntos medios con pequeños segmentos o puntos en el dibujo.

Paso 3: Traza la línea entre los puntos medios

Usando una regla o compás, traza una recta que conecte los puntos medios que has señalado anteriormente. Esta línea será paralela al tercer lado del triángulo y dividirá al triángulo original en dos partes iguales.

Paso 4: Demuestra la igualdad de los segmentos

Para demostrar que el segmento trazado anteriormente es la mediatriz, debes argumentar que los segmentos opuestos formados por la mediatriz son iguales. Puedes utilizar propiedades de congruencia de triángulos, teoremas o axiomas geométricos para hacerlo.

Paso 5: Concluye

Finalmente, escribe una conclusión que resuma el proceso y los resultados obtenidos. Puedes agregar ejemplos adicionales o aplicaciones de la mediatriz en otros problemas geométricos para ampliar aún más el conocimiento del lector.

Demostrar geométricamente que un segmento es la mediatriz de otro en un triángulo requiere la identificación de los puntos medios de los lados del triángulo, la trazada de una línea entre ellos y la demostración de la igualdad de los segmentos generados. Esta técnica es útil en geometría y puede ser aplicada para resolver diversos problemas relacionados con la división de segmentos en partes iguales. Esperamos que este artículo te haya ayudado a comprender mejor cómo sacar la mediatriz de un triángulo.

Hay alguna fórmula específica para calcular la longitud de una mediatriz en un triángulo

Calcular la longitud de una mediatriz en un triángulo puede parecer un desafío, pero en realidad no es tan complicado como parece. Aunque no existe una fórmula específica para calcularla, podemos utilizar algunos conceptos básicos de geometría y propiedades de los triángulos para encontrar esta medida.

Antes de adentrarnos en el cálculo de la mediatriz, recordemos primero qué es exactamente una mediatriz en un triángulo. La mediatriz es una línea perpendicular que pasa por el punto medio de un lado del triángulo y divide al lado en dos segmentos iguales. Si trazamos las tres mediatrices de un triángulo, estas se intersectan en un único punto llamado circuncentro.

Para calcular la longitud de una mediatriz, necesitaremos conocer al menos la información de uno de los lados del triángulo. Supongamos que conocemos la longitud del lado AB, y queremos calcular la longitud de su mediatriz.

Paso 1: Encontrar el punto medio

El primer paso es localizar el punto medio del lado AB. Para hacer esto, simplemente dividimos la longitud del lado AB entre 2. Si tenemos las coordenadas de los puntos A(x₁, y₁) y B(x₂, y₂), podemos usar la fórmula de la distancia entre dos puntos para calcular la longitud del lado AB.

d = √((x₂ - x₁)² + (y₂ - y₁)²)

Una vez que tengamos la longitud del lado AB, la dividimos entre 2 para encontrar el punto medio. Llamemos a este punto M.

Podemos encontrar las coordenadas del punto medio utilizando las siguientes fórmulas:

xₘ = (x₁ + x₂) / 2
yₘ = (y₁ + y₂) / 2

Si conocemos la longitud del lado AB y las coordenadas de los puntos A y B, podemos encontrar fácilmente las coordenadas del punto medio M.

Paso 2: Encontrar la pendiente del lado AB

El segundo paso es calcular la pendiente del lado AB. La pendiente de una recta se calcula como la diferencia en el eje y dividida por la diferencia en el eje x entre dos puntos de la recta.

m = (y₂ - y₁) / (x₂ - x₁)

Utilizando las coordenadas de los puntos A y B, podemos encontrar la pendiente de la recta que pasa por ellos.

Paso 3: Calcular la pendiente perpendicular

Para encontrar la pendiente perpendicular, necesitamos recordar que las líneas mediatrices son perpendiculares a los lados del triángulo. Esto significa que la multiplicación de las pendientes de una mediatriz y su lado correspondiente debe dar -1.

Por lo tanto, para encontrar la pendiente perpendicular, simplemente invertimos la pendiente del lado AB y cambiamos su signo:

mₚ = -1 / m

Donde m es la pendiente calculada en el Paso 2.

Paso 4: Usar la pendiente perpendicular y el punto medio para encontrar la ecuación de la mediatriz

Ahora que conocemos la pendiente perpendicular mₚ y las coordenadas del punto medio M, podemos utilizar la fórmula de la recta para encontrar la ecuación de la mediatriz.

y - yₘ = mₚ(x - xₘ)

Sustituyendo los valores conocidos, podemos obtener la ecuación de la mediatriz.

Paso 5: Calcular la longitud de la mediatriz

Una vez que tengamos la ecuación de la mediatriz en forma general, podemos encontrar la longitud del segmento que representa esta línea. Para hacer esto, necesitamos conocer las coordenadas de los puntos donde la mediatriz intersecta con los otros dos lados del triángulo.

Podemos calcular estas intersecciones utilizando las ecuaciones de las líneas que representan los lados del triángulo y la ecuación de la mediatriz. Resolveremos simultáneamente el sistema de ecuaciones para encontrar los puntos de intersección.

Una vez que tengamos las coordenadas de los puntos de intersección, simplemente utilizamos la fórmula de la distancia entre dos puntos para calcular la longitud de la mediatriz.

Recuerda que este proceso solo nos permite calcular la longitud de una mediatriz si conocemos al menos un lado del triángulo y sus coordenadas correspondientes. Si tenemos información adicional, como la longitud de otro lado o la medida de algún ángulo, podemos utilizar diferentes métodos para encontrar la longitud de la mediatriz.

Aunque no existe una fórmula específica para calcular la longitud de una mediatriz en un triángulo, podemos utilizar el concepto de punto medio, pendiente y ecuación de la recta para encontrar esta medida. Siguiendo los pasos mencionados, podremos resolver nuestras dudas matemáticas y sacar la mediatriz de un triángulo de manera fácil y rápida.

Cuáles son algunos ejemplos prácticos o aplicaciones reales de la mediatriz de un triángulo

La mediatriz de un triángulo es una línea perpendicular que pasa por el punto medio de un lado y divide al triángulo en dos partes iguales. Aunque pueda parecer un concepto abstracto, la mediatriz tiene muchas aplicaciones prácticas y reales en diversas áreas, desde la construcción hasta la navegación.

1. Construcción de estructuras

En arquitectura y construcción, la mediatriz se utiliza para trazar líneas de simetría y encontrar puntos clave de equilibrio en las estructuras. Por ejemplo, al trazar la mediatriz de una viga o un pilar, los constructores pueden determinar con precisión dónde colocar otros elementos estructurales, como soportes o columnas.

2. División de espacios

En diseño de interiores, la mediatriz se utiliza para dividir espacios de manera equitativa y estéticamente agradable. Al trazar la mediatriz de una pared, por ejemplo, los diseñadores pueden determinar dónde colocar objetos decorativos o muebles para lograr un equilibrio visual en la habitación.

3. Navegación marítima

En navegación marítima y aeronáutica, la mediatriz se utiliza para determinar la posición exacta de un objeto en relación con otros puntos de referencia. Por ejemplo, utilizando la mediatriz de dos faros, los navegantes pueden trazar su rumbo y determinar su ubicación actual en el mar.

4. Traslado de coordenadas

En matemáticas y cartografía, la mediatriz se utiliza para calcular y trasladar coordenadas. Al trazar la mediatriz de dos puntos en un mapa, los cartógrafos pueden determinar las coordenadas geográficas exactas de un punto intermedio y trazar rutas o líneas de referencia.

5. Resolución de problemas geométricos

Por supuesto, una de las aplicaciones más directas de la mediatriz es en la resolución de problemas geométricos. Al trazar las mediatrices de un triángulo, los estudiantes pueden encontrar el circuncentro, el punto donde se intersectan las tres mediatrices y que está equidistante a los vértices del triángulo.

La mediatriz de un triángulo tiene múltiples aplicaciones prácticas y reales en diferentes áreas como la construcción, el diseño de interiores, la navegación, las matemáticas y la cartografía. Es un concepto fundamental que nos permite entender y resolver diversos problemas geométricos, así como encontrar puntos clave y equilibrios en diferentes contextos.

La mediatriz de un triángulo es una línea recta que pasa por el punto medio de un lado del triángulo y forma ángulos rectos con dicho lado.

La fórmula para encontrar la ecuación de la mediatriz de un triángulo es y - y1 = m(x - x1), donde (x1, y1) es el punto medio del lado y m es la pendiente del lado.

El punto medio de un lado del triángulo se encuentra promediando las coordenadas de los extremos del lado. Para coordenadas (x1, y1) y (x2, y2), el punto medio es ((x1 + x2)/2, (y1 + y2)/2).

Sí, la mediatriz siempre divide al triángulo en dos partes iguales ya que pasa por el punto medio del lado, que está equidistante de los vértices del triángulo.

No, la longitud de la mediatriz de un triángulo no se puede calcular, ya que es una línea recta infinita que se extiende indefinidamente en ambas direcciones.