Contradominio en matemáticas: Descubre cómo este concepto clave potencia tus conocimientos numéricos

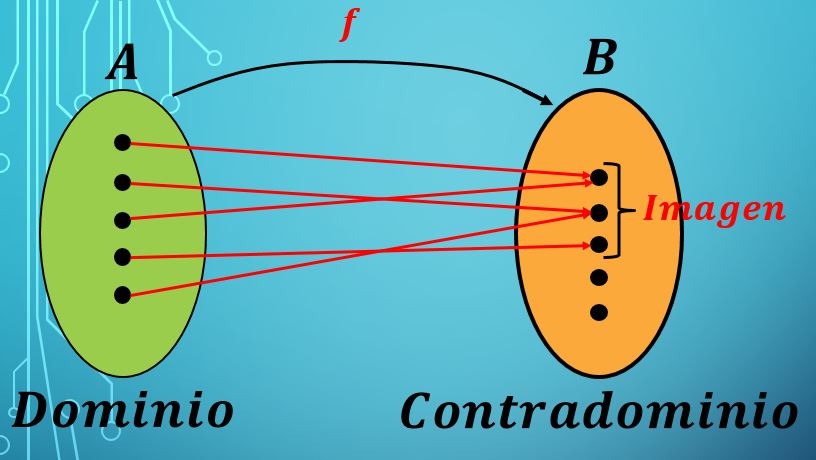
En matemáticas, el contradominio es un concepto clave que se utiliza en la teoría de conjuntos y en el análisis. Se relaciona directamente con las funciones y permite ampliar nuestros conocimientos sobre los números y su comportamiento en diferentes situaciones. Comprender qué es el contradominio nos ayuda a entender mejor las funciones y cómo se relacionan sus elementos.

En este artículo exploraremos en más detalle qué es el contradominio en matemáticas, cuál es su relación con el dominio y el rango, y cómo podemos determinarlo en distintos tipos de funciones. Además, veremos ejemplos prácticos que nos ayudarán a comprender mejor este concepto y su importancia en el análisis matemático. ¡Prepárate para potenciar tus conocimientos numéricos!

Qué es el contradominio en matemáticas y por qué es importante entenderlo

El contradominio es un concepto fundamental en el estudio de las matemáticas. Es una parte esencial del conjunto de definiciones y propiedades que potencian nuestros conocimientos numéricos. Comprender adecuadamente qué es el contradominio y su importancia es clave para resolver problemas matemáticos con precisión y rigurosidad.

Definición del contradominio

Antes de profundizar en la importancia y aplicaciones del contradominio, es necesario entender su definición básica. En matemáticas, el contradominio se refiere al conjunto de todos los valores posibles que puede tomar una función específica. Es decir, es el conjunto de valores a los cuales se pueden asignar los elementos del dominio mediante la función.

Para entender mejor esto, tomemos como ejemplo una función simple. Consideremos la función f(x) = 2x, donde x pertenece al conjunto de números reales. En este caso, el contradominio sería el conjunto de todos los valores reales posibles que pueden obtenerse al evaluar la función f(x). En otras palabras, cualquier número real puede ser el resultado de multiplicar un número real por 2.

Importancia del contradominio

Entender el contradominio es importante porque nos permite tener una visión clara y completa de los posibles resultados de una función. Nos brinda información valiosa sobre cómo se relacionan los elementos del dominio con sus respectivos valores en el contradominio. Además, nos ayuda a determinar si una función es suryectiva o no.

Cuando se trabaja con funciones, es fundamental conocer tanto el dominio como el contradominio. Esto permite definir correctamente la función y evitar errores en su aplicación. Además, el conocimiento del contradominio nos ayuda a interpretar los resultados de una función y comprender su comportamiento en diferentes situaciones.

Aplicaciones del contradominio

El concepto de contradominio tiene numerosas aplicaciones en diversos campos de las matemáticas y otras disciplinas. Algunas áreas destacadas son:

• Análisis funcional: En el análisis funcional, se estudian funciones lineales y no lineales para comprender mejor sus propiedades y comportamiento. El contradominio juega un papel crucial en la descripción de estas funciones y la caracterización de su dominio y rango.
• Álgebra abstracta: En álgebra abstracta, se estudian estructuras algebraicas como grupos, anillos y campos. El contradominio es esencial para definir operaciones y determinar las propiedades de estas estructuras.
• Lógica matemática: En lógica matemática, se utilizan funciones para representar proposiciones y argumentos. El contradominio permite establecer conexiones lógicas entre las variables y analizar la validez de los argumentos.

Estas son solo algunas de las muchas aplicaciones del contradominio en las matemáticas. Su comprensión y manejo adecuado son fundamentales para avanzar en nuestro conocimiento y dominio de esta disciplina.

Cuál es la relación entre el contradominio y el dominio en una función

El contradominio es un concepto fundamental en matemáticas que está estrechamente relacionado con el dominio de una función. Antes de explorar la relación entre estos dos conceptos, es importante comprender qué se entiende por cada uno de ellos.

El dominio de una función es el conjunto de todos los valores de entrada para los cuales la función está definida. En otras palabras, es el conjunto de valores que podemos ingresar en la función y obtener un resultado válido. Por ejemplo, si tenemos la función f(x) = x^2, el dominio sería todos los números reales, ya que podemos elevar al cuadrado cualquier número real y obtener un resultado válido.

Por otro lado, el contradominio es el conjunto de todos los valores posibles de salida de una función. Es decir, son todos los valores a los que la función puede mapear los elementos de su dominio. Siguiendo con el ejemplo anterior, el contradominio de la función f(x) = x^2 también serían todos los números reales, ya que cualquier número real puede ser el resultado de elevar al cuadrado otro número real.

Ahora que entendemos qué es el dominio y el contradominio por separado, podemos explorar su relación en una función. La relación entre ambos conceptos radica en la forma en que se definen conjuntamente. En una función bien definida, el contradominio será un subconjunto del dominio. Esto se debe a que no todas las posibles salidas pueden ser alcanzadas por la función, solo aquellas que están dentro de su contradominio.

Por ejemplo, consideremos la función g(x) = √x. El dominio de esta función sería el conjunto de números reales no negativos, ya que no podemos calcular la raíz cuadrada de un número negativo en los números reales. Sin embargo, el contradominio de esta función sería el conjunto de números reales, porque al evaluar la función para cualquier número real no negativo, obtendríamos un resultado válido.

Es importante tener en cuenta que, aunque el contradominio es un subconjunto del dominio, puede haber elementos en el dominio que no estén mapeados por la función y, por lo tanto, no estarán presentes en el contradominio. Estos son conocidos como valores no alcanzables o valores no abarcados por la función.

El contradominio es un concepto clave en matemáticas que se relaciona estrechamente con el dominio de una función. Mientras que el dominio define los valores de entrada posibles, el contradominio establece todos los valores de salida alcanzables por la función. Es importante entender cómo estos dos conceptos trabajan juntos para tener una comprensión completa de las funciones matemáticas.

Cómo se determina el contradominio de una función dada

El contradominio es un concepto fundamental en matemáticas que nos permite determinar de manera precisa la extensión posible de los valores de salida de una función. Para comprender cómo se calcula el contradominio de una función dada, primero debemos entender qué es el dominio y el codominio.

El dominio de una función se refiere al conjunto de todos los valores de entrada posibles para esa función. Es decir, son los valores que podemos "meter" dentro de la función y obtener un resultado válido. Por otro lado, el codominio de una función es el conjunto de todos los valores de salida que puede tomar la función.

Una vez que tenemos claridad sobre el dominio y el codominio, podemos proceder a calcular el contradominio. El contradominio representa el conjunto de valores de salida que realmente toma la función en la práctica. Es importante tener en cuenta que el contradominio no siempre coincide con el codominio de la función.

Para determinar el contradominio, podemos seguir estos pasos:

1. Analizar los valores de salida de la función: Toma nota de los distintos valores de salida que la función experimenta en su rango de números de entrada. Observa si hay algún patrón o tendencia evidente.
2. Considerar los límites de la función: En algunos casos, es posible identificar límites superiores e inferiores para los valores de salida de la función. Estos límites pueden ser determinados por características propias de la función o por restricciones impuestas en el enunciado del problema.
3. Revisar las restricciones adicionales: Algunas funciones pueden tener restricciones adicionales impuestas por el problema o contexto específico en el que se apliquen. Estas restricciones pueden limitar los valores de salida posibles.

Una vez que hayamos realizado estos pasos, podremos determinar con mayor precisión el contradominio de la función. Es importante recordar que el contradominio está directamente relacionado con los valores de salida específicos que la función puede tomar en la práctica, y no necesariamente incluye todos los valores potenciales dentro del codominio.

Ejemplo de cálculo del contradominio:

Supongamos que tenemos la siguiente función:

f(x) = x^2 + 3x - 2

Para calcular el contradominio de esta función, podemos seguir los pasos antes mencionados:

1. Analizando los valores de salida: Al graficar la función o evaluar diferentes valores de entrada, podemos observar que la función siempre produce resultados positivos o nulos. Esto nos indica que el contradominio estará compuesto por valores mayores o igual a cero.
2. Límites de la función: En este caso, no hay límites superiores ni inferiores explícitos, ya que la función es una parábola ascendente.
3. Restricciones adicionales: No hay restricciones adicionales impuestas en este ejemplo.

En base a estos pasos, podemos determinar que el contradominio de la función f(x) = x^2 + 3x - 2 es el conjunto de todos los números reales mayores o iguales a cero.

El contradominio nos permite conocer con exactitud los valores de salida que una función puede tomar en la práctica. Mediante un análisis cuidadoso y considerando factores como los valores de salida, límites y restricciones adicionales, podemos calcular el contradominio de manera precisa. Esta información es fundamental para comprender mejor el comportamiento de las funciones y potenciar nuestros conocimientos numéricos en matemáticas.

Qué papel juega el contradominio en el análisis de funciones y sus gráficas

El contradominio es un concepto fundamental en el análisis de funciones y sus gráficas. Nos permite comprender la relación entre los conjuntos de entrada y salida de una función y cómo se puede representar de manera visual mediante una gráfica. Entender el papel del contradominio nos ayuda a potenciar nuestros conocimientos numéricos y nos brinda herramientas para resolver problemas matemáticos con mayor precisión.

En primer lugar, es importante entender qué es el contradominio en el contexto de las funciones. El contradominio es el conjunto de todos los posibles valores de salida de una función. En otras palabras, es el conjunto de valores hacia los cuales la función puede mapear los valores de su dominio. Este conjunto puede ser más grande que el rango de la función, ya que algunos valores pueden no tener una imagen correspondiente en el codominio.

Para visualizar mejor esto, podemos utilizar una analogía con un mapa. Imagina que estás buscando una ubicación específica en un mapa y quieres saber todos los lugares posibles a los que puedes llegar. El mapa en sí representa el contradominio, mientras que tu punto de partida y destino final representan el dominio y el rango respectivamente. El contradominio te muestra todas las posibles opciones a las que puedes llegar desde tu punto de partida, aunque es posible que no llegues a todos estos lugares.

Importancia del contradominio en el análisis de funciones

El estudio del contradominio es esencial para comprender las propiedades de una función y su comportamiento en diferentes situaciones. Al conocer el contradominio de una función, podemos determinar si hay restricciones en los valores de entrada y salida, lo que puede ayudarnos a evitar errores en nuestros cálculos y predicciones.

Además, el contradominio nos permite identificar si una función es sobreyectiva, es decir, si cada elemento del contradominio tiene al menos un elemento en el dominio que lo mapea. Esto es importante para establecer la biyectividad de una función y su inversa. Si el contradominio no está completamente cubierto por el rango de la función, esto indica que la función no es sobreyectiva y podemos tener problemas al intentar encontrar su inversa.

El contradominio también es relevante en el análisis de las gráficas de funciones. Al trazar una gráfica, es necesario tener en cuenta el conjunto de valores hacia los cuales la función puede mapear los valores de su dominio. Esta información nos ayuda a determinar el rango de la función y a visualizar cómo se comporta en diferentes intervalos. Además, al conocer el contradominio, podemos identificar puntos de discontinuidad o de inflexión que pueden afectar la representación gráfica de la función.

El contradominio es un concepto esencial en el análisis de funciones y sus gráficas. Nos permite comprender la relación entre el dominio y el rango de una función, así como identificar restricciones y propiedades importantes. Conocer el contradominio nos brinda herramientas valiosas para resolver problemas matemáticos con mayor precisión y realizar representaciones gráficas más precisas. Es fundamental tener en cuenta este concepto para potenciar nuestros conocimientos numéricos y mejorar nuestra comprensión de las funciones en el campo de las matemáticas.

Qué sucede cuando el contradominio no coincide con el rango de una función

El contradominio es un concepto fundamental en matemáticas que se relaciona directamente con el rango de una función. Cuando hablamos de una función, nos referimos a una relación entre dos conjuntos, llamados dominio y contradominio, que asigna a cada elemento del dominio un único elemento del contradominio.

En términos más sencillos, el contradominio representa todos los posibles valores de salida de una función. Es decir, son aquellos valores que puede tomar la variable dependiente cuando se sustituyen los valores del dominio en la función.

Ahora bien, ¿qué ocurre cuando el contradominio no coincide con el rango de una función? Esto implica que existen elementos en el contradominio que no tienen ningún correspondiente en el rango de la función. En otras palabras, la función no es capaz de alcanzar ciertos valores dentro de su contradominio.

¿Cuándo sucede esto?

Existen varias situaciones en las cuales el contradominio puede no coincidir con el rango de una función. Una de ellas es cuando la función no está definida para ciertos valores del dominio. Por ejemplo, si tenemos una función que representa la altura de una persona en función de su edad, es posible que dicha función no esté definida para edades negativas o edades muy avanzadas. En este caso, el contradominio podría ser el conjunto de números reales, pero el rango de la función se restringiría a un subconjunto específico dentro de ese conjunto.

Otra situación común es cuando la función tiene restricciones adicionales, como una condición de paridad. Por ejemplo, si consideramos una función que representa el área de un círculo en función de su radio, es posible que dicha función solo esté definida para radios no negativos. En este caso, el contradominio sería el conjunto de números reales no negativos, pero el rango de la función se limitaría a los valores positivos.

También debemos tener en cuenta que existen funciones que son invertibles, es decir, funciones que tienen una correspondencia biunívoca entre el dominio y el contradominio. En estos casos, el contradominio coincidirá siempre con el rango de la función, ya que cada valor del contradominio tendrá exactamente un valor correspondiente en el rango de la función.

Implicaciones y aplicaciones

Comprender la relación entre el contradominio y el rango de una función es de vital importancia en diversas áreas de las matemáticas y de otras disciplinas. Por ejemplo, en el ámbito de la programación, entender las restricciones y limitaciones de una función nos permite desarrollar algoritmos más eficientes y evitar errores o comportamientos inesperados. Del mismo modo, en el análisis de datos, conocer el contradominio de una función nos ayuda a interpretar correctamente los resultados obtenidos y tomar decisiones informadas sobre el tratamiento de la información.

Además, el estudio del contradominio en matemáticas nos permite ampliar nuestro conocimiento sobre la estructura y propiedades de las funciones, así como profundizar en conceptos como la continuidad, la diferenciabilidad y la integrabilidad. Entender cómo el contradominio determina las posibles salidas de una función nos brinda una perspectiva más completa y rigurosa del funcionamiento de los sistemas numéricos.

El contradominio es un concepto esencial en matemáticas que nos ayuda a comprender las limitaciones y alcances de una función. Cuando el contradominio no coincide con el rango de una función, se generan situaciones particulares que requieren de un análisis detallado. A través del estudio y la aplicación de este concepto, podemos potenciar nuestros conocimientos numéricos y mejorar nuestra comprensión de las relaciones entre variables en diferentes contextos.

Puedes dar ejemplos prácticos de cómo trabajar con el contradominio en problemas matemáticos

El contradominio es un concepto clave en matemáticas que nos permite potenciar nuestros conocimientos numéricos y resolver problemas de una manera más efectiva. En este artículo, te mostraremos algunos ejemplos prácticos de cómo trabajar con el contradominio y cómo aplicarlo en situaciones reales.

Ejemplo 1: Funciones lineales

Para entender mejor cómo funciona el contradominio, consideremos una función lineal simple. Supongamos que tenemos la función f(x) = 2x+1, donde x representa un número real. El dominio de esta función sería todos los números reales, ya que no hay restricciones en cuanto a qué valores de x podemos utilizar.

Sin embargo, el contradominio de esta función es un poco más restrictivo. Para determinar el contradominio, debemos considerar la imagen de la función, es decir, los valores posibles que toma f(x). En este caso, podemos ver que la función genera valores para cualquier número real cuando le damos diferentes valores a x.

Por lo tanto, el contradominio de esta función sería también todos los números reales.

Ejemplo 2: Funciones cuadráticas

Veamos ahora un ejemplo con una función cuadrática, como f(x) = x^2. Nuevamente, el dominio de esta función sería todos los números reales. Sin embargo, al examinar la imagen de la función, nos damos cuenta de que solo produce valores no negativos.

Entonces, el contradominio de esta función sería el conjunto de números reales no negativos.

Ejemplo 3: Funciones trigonométricas

Consideremos ahora una función trigonométrica, como f(x) = sen(x). El dominio de esta función sería todos los números reales, ya que el seno está definido para cualquier ángulo.

Sin embargo, el contradominio de esta función estaría entre -1 y 1, ya que esos son los valores posibles que puede tomar el seno de un ángulo.

El contradominio nos ayuda a entender cuáles son los posibles valores de una función específica. Al determinar el contradominio, debemos considerar la imagen de la función y los valores que produce. Esto nos permite resolver problemas matemáticos de manera más precisa y eficiente.

Cómo el concepto de contradominio puede ayudarme a resolver ecuaciones y desigualdades numéricas

El concepto de contradominio es fundamental en matemáticas, especialmente cuando se trata de resolver ecuaciones y desigualdades numéricas. Comprender el papel del contradominio nos permite realizar operaciones y encontrar soluciones de manera más precisa y efectiva.

En su forma más básica, el contradominio se refiere al conjunto de todos los posibles valores que puede tomar una función. En otras palabras, es el rango de valores que la variable dependiente puede tener como resultado de la función. Este concepto es particularmente útil cuando trabajamos con funciones que tienen restricciones o condiciones específicas para los valores de entrada.

Un ejemplo práctico

Imaginemos que tenemos una función f(x) = x^2, donde x representa los números reales. Cuando graficamos esta función, obtenemos una parábola que se abre hacia arriba.

Si no establecemos ningún tipo de restricción para los valores de x, podemos decir que el contradominio de esta función es el conjunto de todos los números reales. Esto significa que cualquier número real puede ser resultado de evaluar la función f(x) en algún valor específico de x.

Sin embargo, hay ocasiones en las que queremos trabajar con funciones que tienen limitaciones o condiciones específicas. Por ejemplo, si queremos encontrar los valores de x que hacen que f(x) sea mayor o igual a 9, estamos estableciendo una restricción. En este caso, solo nos interesan los valores de x que satisfacen esta condición.

De esta manera, el contradominio cambia y se restringe a un subconjunto de los números reales. En este ejemplo, el contradominio sería el conjunto de todos los números reales mayores o iguales a 9.

Cómo utilizar el concepto de contradominio en la resolución de ecuaciones y desigualdades numéricas

El concepto de contradominio nos brinda una guía clara para resolver ecuaciones y desigualdades numéricas. Cuando se nos presenta una ecuación o desigualdad, podemos identificar y definir el contradominio apropiado en función de las restricciones o condiciones establecidas.

Al establecer el contradominio, nos estamos enfocando solo en los valores que son relevantes para la solución del problema. Esto nos ayuda a simplificar el proceso de encontrar los posibles valores de la variable dependiente que satisfacen la ecuación o desigualdad dada.

Una vez que hemos determinado el contradominio, podemos utilizar diversas estrategias y técnicas para resolver la ecuación o desigualdad. Estas pueden incluir realizar operaciones algebraicas, aplicar propiedades y teoremas matemáticos, o incluso graficar la función correspondiente para visualizar la solución.

Es importante tener en cuenta que el contradominio puede influir en el tipo y número de soluciones que encontramos. Al restringir los posibles valores de la variable dependiente, podemos obtener un conjunto de soluciones más preciso y significativo.

El concepto de contradominio es esencial para resolver ecuaciones y desigualdades numéricas debido a su capacidad para delimitar los posibles valores de la variable dependiente. Al establecer el contradominio, podemos enfocarnos en los valores relevantes y así simplificar la búsqueda de soluciones.

Además, comprender el contradominio nos ayuda a desarrollar un sentido más profundo de cómo funcionan las funciones y cómo se relacionan con los números reales. Esto nos permite utilizar estrategias más efectivas para resolver problemas matemáticos y potenciar nuestros conocimientos numéricos.

Existen límites para el contradominio en matemáticas? ¿Qué ocurre cuando se trabaja con números infinitos o imaginarios

El contradominio es un concepto fundamental en matemáticas que nos permite entender mejor la relación entre conjuntos. Cuando trabajamos con números reales, el contradominio se define como el conjunto de todos los posibles valores de salida de una función dada. Pero ¿qué ocurre cuando hablamos de números infinitos o imaginarios?

Cuando nos adentramos en el ámbito de los números infinitos, el concepto de contradominio se extiende para incluir todos los valores que se pueden obtener como resultado de una función en este conjunto numérico. Es importante destacar que, a diferencia de los números reales, los números infinitos no tienen límites definidos, por lo que su contradominio puede ser considerado infinitamente grande.

Por otro lado, cuando trabajamos con números imaginarios, el contradominio se amplía aún más. Los números imaginarios son aquellos que tienen una parte real igual a cero y una parte imaginaria distinta de cero, representada por la unidad imaginaria "i". En este caso, el contradominio estará compuesto por todos los números complejos que se obtienen como resultado de la función.

La importancia del contradominio en matemáticas

El estudio del contradominio es esencial en matemáticas, ya que nos permite comprender la relación entre los elementos de un conjunto de partida y su correspondencia con los valores de salida de una función. Esta relación es especialmente relevante en áreas como el análisis matemático, donde se busca entender cómo cambian los valores de una función en función de sus variables.

Al conocer el contradominio de una función, podemos determinar cuáles son los posibles resultados que se pueden obtener al evaluar dicha función. Esto nos ayuda a entender mejor el comportamiento de la función y nos proporciona información valiosa sobre los diferentes valores que puede tomar.

El papel del contradominio en problemas matemáticos

El concepto de contradominio también es fundamental para abordar problemas matemáticos más complejos. Al analizar las propiedades del contradominio, podemos determinar si una función cumple con ciertas condiciones o requerimientos específicos.

Por ejemplo, supongamos que estamos trabajando en el campo de la criptografía, donde se utilizan funciones matemáticas para garantizar la seguridad de las comunicaciones. En este caso, es crucial conocer el contradominio de una función para asegurarnos de que la información cifrada solo pueda ser desencriptada por aquellos que poseen la clave correcta.

• El contradominio nos permite limitar el rango de posibles resultados y garantizar la integridad y confidencialidad de la información.
• Además, al comprender qué valores pueden tomar las variables de una función en relación con su contradominio, podemos plantear y resolver ecuaciones y sistemas de ecuaciones de manera más efectiva.

El contradominio es un concepto clave en matemáticas que nos ayuda a entender la relación entre conjuntos y cómo se comportan las funciones. Ya sea trabajando con números reales, infinitos o imaginarios, el conocimiento del contradominio nos brinda una herramienta poderosa para potenciar nuestros conocimientos numéricos y abordar problemas matemáticos de manera más eficiente.

Cuáles son algunas aplicaciones del concepto de contradominio en áreas como la física, la economía o la informática

El concepto de contradominio es fundamental en diversas ramas del conocimiento, como la física, la economía y la informática. En estas disciplinas, el contradominio se utiliza para potenciar los conocimientos numéricos y obtener resultados más precisos.

Física

En física, el concepto de contradominio se emplea en diferentes áreas, como la termodinámica, la mecánica cuántica o la electromagnética. Por ejemplo, en la mecánica cuántica, el contradominio permite determinar las posibles soluciones a una ecuación de onda, lo que resulta crucial para comprender el comportamiento de partículas subatómicas.

Además, en la termodinámica, el contradominio se utiliza para calcular magnitudes como la entropía o la temperatura, permitiendo un análisis más riguroso de los sistemas termodinámicos y su evolución en el tiempo.

Economía

En el campo de la economía, el concepto de contradominio desempeña un papel esencial en el análisis de variables económicas y financieras. Por ejemplo, en la valoración de activos financieros, el contradominio se utiliza para establecer el rango de posibles valores que puede tomar una variable, como el precio de una acción o el tipo de interés de un préstamo.

Asimismo, en la modelización de fenómenos económicos, el contradominio permite definir las restricciones y condiciones que deben cumplirse en un sistema económico, lo cual ayuda a determinar las soluciones óptimas desde el punto de vista económico.

Informática

En el ámbito de la informática, el concepto de contradominio es clave en el diseño y desarrollo de algoritmos, bases de datos y sistemas de información. Por ejemplo, en el diseño de una base de datos, el contradominio se utiliza para definir los posibles valores que puede tomar un atributo, lo cual facilita la estructuración y organización de los datos.

Además, en la programación, el contradominio permite establecer las condiciones necesarias para que un programa cumpla con su objetivo y genere resultados válidos y precisos. Esto resulta especialmente importante en áreas como la inteligencia artificial, donde el uso correcto del contradominio garantiza la fiabilidad de los algoritmos y modelos utilizados.

El concepto de contradominio tiene múltiples aplicaciones en campos tan diversos como la física, la economía y la informática. Su comprensión y correcta utilización permiten potenciar los conocimientos numéricos y obtener resultados más precisos en estas disciplinas.

Cuál es el siguiente paso después de comprender el contradominio en matemáticas? ¿Hay otros conceptos relacionados que también debería explorar

Una vez que hayas comprendido el concepto de contradominio en matemáticas, es importante tener en cuenta que existen otros conceptos relacionados que también debes explorar para potenciar tus conocimientos numéricos.

1. Dominio

El dominio se refiere al conjunto de todos los valores de entrada posibles para una función matemática. Es decir, son los valores que puedes ingresar en una función para obtener un resultado válido. Comprender y definir el dominio es fundamental para comprender por completo el contradominio.

2. Codominio

El codominio, por otro lado, se refiere al conjunto de todos los valores de salida posibles para una función matemática. Es decir, son los valores que pueden ser obtenidos como resultado de aplicar la función a los valores del dominio. El codominio puede ser más amplio que el rango de una función, ya que podría incluir valores que no son alcanzados en realidad.

3. Rango

El rango es el conjunto de todos los valores que realmente son alcanzados como resultado de aplicar una función a los valores del dominio. Es decir, son los valores de salida reales obtenidos a partir de una función. Comprender el rango es esencial para entender cómo se relaciona con el contradominio y para identificar si una función es sobreyectiva o no.

4. Relación entre el contradominio, codominio y rango

La relación entre el contradominio, codominio y rango puede ser confusa al principio. Sin embargo, es importante recordar que el contradominio es el conjunto de valores posibles para los resultados de una función, el codominio es el conjunto de valores que pueden ser obtenidos como resultado de aplicar la función y el rango es el conjunto de valores que realmente se obtienen como resultado. El contradominio abarca tanto el codominio como el rango, pero estos últimos dos pueden no ser iguales.

Por ejemplo, considera la siguiente función:

f(x) = x^2

El dominio de esta función puede ser cualquier número real, ya que no hay restricciones en la entrada. El codominio también puede ser cualquier número real, ya que al elevar cualquier número real al cuadrado se obtiene un número real. Sin embargo, el rango de esta función solo incluirá los números reales no negativos, ya que no se pueden obtener resultados negativos al elevar al cuadrado.

Explorar y comprender la relación entre el contradominio, codominio y rango te ayudará a comprender mejor las propiedades de las funciones y a realizar análisis más profundos sobre su comportamiento y características.

5. Aplicaciones prácticas del contradominio

Aunque puede parecer un concepto abstracto en matemáticas, el contradominio tiene diversas aplicaciones prácticas en varias áreas. Por ejemplo, en ciencias de la computación, el contradominio es fundamental para comprender el funcionamiento de algoritmos y programación. En física, el contradominio es esencial para analizar el movimiento de los objetos y predecir su comportamiento. En economía y negocios, el contradominio juega un papel importante en el análisis de datos y la toma de decisiones basada en modelos matemáticos.

Comprender el contradominio en matemáticas es solo el primer paso para potenciar tus conocimientos numéricos. Explorar conceptos relacionados como el dominio, codominio y rango te permitirá adquirir un entendimiento más completo sobre las funciones matemáticas y sus aplicaciones prácticas en diferentes disciplinas.

Preguntas frecuentes (FAQ)

¿Qué es el contradominio en matemáticas?

El contradominio es el conjunto de todos los posibles valores que puede tomar la función.

¿Cuál es la diferencia entre contradominio y codominio?

El contradominio incluye todos los posibles valores de salida de una función, mientras que el codominio solo incluye los valores a los que realmente llega la función.

¿Cómo se determina el contradominio de una función?

Para determinar el contradominio de una función, debes identificar todos los posibles valores que pueden salir de la función. Esto se puede hacer analizando la fórmula de la función y su dominio.

¿Por qué es importante el contradominio?

El contradominio es importante porque permite conocer todos los potenciales valores de salida de una función, lo cual es necesario para entender completamente cómo se comporta la función.

¿Cuál es la relación entre el contradominio y el rango de una función?

El rango de una función es un subconjunto del contradominio. El rango son los valores a los que efectivamente llega la función, mientras que el contradominio incluye todos los posibles valores.