Cuando una matriz no tiene inversa: Descubre las razones y consecuencias de esta propiedad crucial

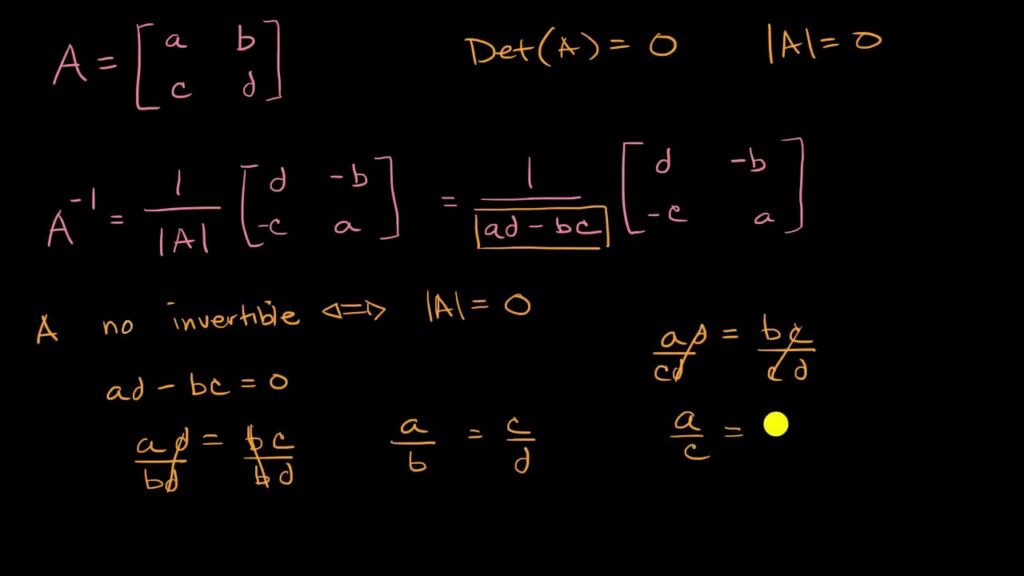
En el ámbito de las matemáticas, una matriz es un arreglo rectangular de números organizados en filas y columnas. Las matrices tienen muchas aplicaciones tanto en la teoría como en la práctica, siendo utilizadas en diversos campos como la física, la economía y la informática. Una propiedad importante de las matrices es su inversa, que permite resolver ecuaciones lineales y realizar operaciones algebraicas. Sin embargo, no todas las matrices tienen inversa, lo cual puede tener implicaciones significativas.

Exploraremos las razones por las cuales una matriz puede no tener inversa. Examinaremos diferentes escenarios y condiciones para comprender por qué algunas matrices no pueden ser invertidas. Además, analizaremos las consecuencias de esta propiedad y cómo afecta a las operaciones matemáticas que se pueden realizar con estas matrices. Comprender por qué una matriz no tiene inversa es fundamental para evitar errores al trabajar con ellas y permite obtener soluciones más precisas y confiables en problemas matemáticos.

Qué es una matriz inversa y por qué es importante

Una matriz inversa es aquella que, cuando se multiplica por la matriz original, produce la identidad. Es decir, si A es una matriz cuadrada de tamaño nxn, entonces su matriz inversa, denotada como A^(-1), tendrá la propiedad de que A * A^(-1) = I, donde I es la matriz identidad de tamaño nxn.

La existencia de una matriz inversa es un concepto fundamental en el álgebra lineal y tiene varias aplicaciones importantes en diversas ramas de las matemáticas y la física. Por ejemplo, cuando resolvemos sistemas de ecuaciones lineales, podemos utilizar la matriz inversa para encontrar la solución exacta. Además, la matriz inversa también juega un papel crucial en el cálculo de determinantes, la resolución de ecuaciones diferenciales y el estudio de transformaciones lineales.

La importancia de la matriz inversa radica en su propiedad para deshacer los efectos de la matriz original. Si tenemos una transformación lineal representada por una matriz A, su inversa nos permite regresar a los valores originales antes de la transformación. Esto resulta especialmente útil en problemas donde necesitamos deshacer una serie de transformaciones y volver al estado inicial.

Razones por las cuales una matriz puede no tener inversa

Aunque la mayoría de las matrices cuadradas tienen una matriz inversa, existen casos particulares en los cuales una matriz no posee inversa. Estas son algunas de las razones más comunes:

• Matriz singular: Una matriz es singular si su determinante es igual a cero. En este caso, la matriz no tiene inversa porque no se puede deshacer la transformación lineal que representa.
• Matriz no cuadrada: Solo las matrices cuadradas pueden tener una matriz inversa. Si una matriz no es cuadrada, automáticamente se descarta la posibilidad de que tenga una matriz inversa.

Estas son solo algunas de las razones por las cuales una matriz puede no tener inversa. La falta de inversa puede limitar las operaciones algebraicas y el análisis matemático que se pueden realizar con dicha matriz. Es importante considerar estas propiedades al trabajar con matrices en diferentes contextos.

Cuándo una matriz no tiene inversa y por qué ocurre esto

En el ámbito de las matemáticas y la álgebra lineal, una propiedad fundamental de las matrices es su capacidad para tener una inversa. Sin embargo, hay casos en los que una matriz no tiene inversa. En esta sección, exploraremos las razones por las cuales esto ocurre y las consecuencias que tiene esta propiedad crucial.

Para comprender por qué una matriz puede carecer de inversa, debemos entender primero qué es una matriz invertible. Una matriz cuadrada A se considera invertible si existe otra matriz cuadrada B tal que el producto de A y B resulte en la identidad, es decir, AB = BA = I, donde I es la matriz identidad.

Ahora bien, una de las razones principales por las cuales una matriz no tiene inversa es porque es singular, es decir, su determinante es igual a cero. El determinante de una matriz proporciona información valiosa sobre sus propiedades y características.

Si el determinante de una matriz es cero, es imposible encontrar una matriz inversa, ya que la operación de división no sería válida. Esta propiedad tiene importantes implicaciones en diversas áreas como la resolución de sistemas de ecuaciones lineales y la diagonalización de matrices, entre otras.

Otra razón por la cual una matriz puede carecer de inversa es porque sus filas o columnas son linealmente dependientes. Esto implica que una o más filas o columnas pueden expresarse como combinaciones lineales de otras filas o columnas de la matriz.

Cuando esto ocurre, existen infinitas soluciones posibles para el sistema de ecuaciones lineales asociado a la matriz, lo que impide que la matriz tenga una única matriz inversa. Esta propiedad puede afectar la resolución de problemas prácticos en áreas como la ingeniería y la física, donde el cálculo preciso de las soluciones es fundamental.

Hay dos razones principales por las cuales una matriz puede carecer de inversa: su determinante es cero o sus filas/columnas son linealmente dependientes. Estas propiedades tienen consecuencias significativas en distintos campos de estudio y aplicaciones prácticas. Al comprender las razones y las implicaciones de esta propiedad crucial, podemos abordar problemas matemáticos y de ingeniería con mayor precisión y eficacia.

Cuáles son las razones más comunes por las que una matriz no tiene inversa

Cuando se estudia álgebra lineal, una propiedad crucial es la inversibilidad de las matrices. Sin embargo, existen casos en los que una matriz no tiene inversa y es importante comprender las razones detrás de esta situación.

Una de las razones más comunes por las que una matriz no tiene inversa es porque su determinante es igual a cero. El determinante es un número que se calcula a partir de los coeficientes de la matriz y nos indica si ésta puede ser invertida o no. Si el determinante es igual a cero, significa que los coeficientes de la matriz están relacionados entre sí de tal manera que no es posible deshacer sus operaciones y encontrar una solución única.

Otra razón por la cual una matriz puede no tener inversa es si alguna de sus filas o columnas son linealmente dependientes. Esto significa que una fila o columna puede ser expresada como combinación lineal de las demás. En este caso, no existe una solución única para la matriz y, por lo tanto, no puede ser invertida.

Además, cuando una matriz tiene filas o columnas que son todas nulas, tampoco tendrá inversa. Esto se debe a que no hay suficiente información en la matriz para deshacer las operaciones y encontrar una matriz inversa.

Es importante destacar que, aunque una matriz no tenga inversa, esto no implica necesariamente que sea inútil. Por ejemplo, en sistemas de ecuaciones lineales, una matriz no invertible puede representar una situación en la que no hay una solución única, pero puede haber múltiples soluciones o incluso infinitas.

Las consecuencias de una matriz no invertible son importantes de tener en cuenta. Por ejemplo, en problemas de optimización, una matriz invertible garantiza que se pueda encontrar un máximo o mínimo de una función. Sin embargo, si la matriz no tiene inversa, es posible que no se pueda obtener un resultado válido.

Las razones más comunes por las que una matriz no tiene inversa son: un determinante igual a cero, filas o columnas linealmente dependientes y filas o columnas nulas. Es crucial comprender estas razones y sus consecuencias para poder utilizar correctamente las matrices en diversas aplicaciones matemáticas y científicas.

Cómo puedo determinar si una matriz tiene o no tiene inversa

Para determinar si una matriz tiene inversa o no, es necesario entender qué significa que una matriz tenga inversa. En términos simples, si una matriz A tiene una matriz inversa A^-1, entonces el producto de A y A^-1 es igual a la identidad, es decir, A * A^-1 = I.

Existen diferentes métodos para determinar si una matriz tiene inversa:

Método del determinante

• Para una matriz cuadrada A, podemos calcular su determinante det(A).
• Si det(A) es diferente de cero, entonces la matriz tiene inversa.
• Si det(A) es igual a cero, entonces la matriz no tiene inversa.

Método de la matriz adjunta

• Podemos calcular la matriz adjunta de A, denotada como adj(A).
• Si la matriz adjunta de A tiene un determinante diferente de cero, entonces A tiene inversa.
• Si la matriz adjunta de A tiene un determinante igual a cero, entonces A no tiene inversa.

Método de eliminación gaussiana

• Podemos realizar operaciones de fila en la matriz A utilizando el método de eliminación gaussiana para llevar la matriz a su forma escalonada reducida.
• Si después de aplicar las operaciones de fila, obtenemos una matriz escalonada reducida con todas sus filas principales son no nulas, entonces la matriz tiene inversa.
• Si después de aplicar las operaciones de fila, obtenemos una matriz escalonada reducida con alguna fila principal nula, entonces la matriz no tiene inversa.

Estos son solo algunos métodos comunes para determinar si una matriz tiene o no tiene inversa. Es importante destacar que una matriz cuadrada solo puede tener una inversa si su determinante es diferente de cero. La propiedad de tener inversa es crucial en muchas áreas de las matemáticas y se utiliza en numerosos cálculos y aplicaciones prácticas.

Cuáles son las consecuencias de no tener una matriz inversa en un sistema de ecuaciones lineales

La existencia de una matriz inversa en un sistema de ecuaciones lineales es una propiedad fundamental que tiene importantes implicaciones en el ámbito matemático. Sin embargo, en algunos casos particulares, nos encontramos con matrices que no tienen inversa. En esta sección, vamos a analizar cuáles son las consecuencias de esta falta de inversa y cómo afecta a la solución de un sistema de ecuaciones.

Razones por las que una matriz no tiene inversa

Existen distintas razones por las cuales una matriz puede carecer de inversa. La más común es cuando su determinante es igual a cero. Recordemos que el determinante de una matriz es un número que nos proporciona información sobre las propiedades de dicha matriz. Cuando el valor del determinante es cero, significa que la matriz no tiene inversa.

Otra razón puede ser que la matriz no sea cuadrada, ya que solo las matrices cuadradas tienen la posibilidad de tener inversa. Las matrices no cuadradas no cumplen los requisitos necesarios para que exista una inversa definida.

Además, una matriz puede no tener inversa si sus columnas o filas son linealmente dependientes. Esto significa que una o varias columnas/filas pueden ser expresadas como combinaciones lineales de las demás, lo cual impide la existencia de una matriz inversa única.

Consecuencias de la falta de inversa en un sistema de ecuaciones lineales

Cuando nos enfrentamos a un sistema de ecuaciones lineales cuya matriz de coeficientes no tiene inversa, esto implica que dicho sistema no tiene solución única. Esto se debe a que la inversa de una matriz nos permite encontrar una solución única para el sistema de ecuaciones.

En lugar de tener una solución única, podemos encontrarnos con varias posibilidades:

• El sistema puede tener infinitas soluciones.
• El sistema puede ser inconsistente, es decir, no tener solución alguna.

Si el sistema tiene infinitas soluciones, esto implica que existen múltiples combinaciones lineales de las variables que satisfacen todas las ecuaciones del sistema. Estas soluciones formarán un espacio vectorial dentro del espacio donde se encuentran las variables del sistema.

Por otro lado, si el sistema no tiene solución, significa que las ecuaciones son contradictorias y no existe ninguna combinación lineal de las variables que pueda satisfacer todas las ecuaciones del sistema. En este caso, decimos que las ecuaciones son inconsistentes y representan un problema sin solución.

Ejemplos de sistemas sin inversa y sus consecuencias

Para ilustrar estas ideas, consideremos el siguiente sistema de ecuaciones:


2x + 3y = 6
4x + 6y = 12


Si representamos este sistema en forma matricial, obtendremos:


| 2 3 | | x | | 6 |
| 4 6 | * | y | = | 12 |


Calculando el determinante de la matriz de coeficientes, obtenemos:


2 * 6 - 3 * 4 = 0


Como el determinante es igual a cero, podemos concluir que esta matriz no tiene inversa. Por lo tanto, las consecuencias en este caso son:

• El sistema puede tener infinitas soluciones o puede ser inconsistente.
• Las ecuaciones representan un problema sin una solución única.

Cuando una matriz no tiene inversa, esto implica que el sistema de ecuaciones lineales asociado no tiene una solución única. Esta falta de inversa puede deberse al valor del determinante, a que la matriz no sea cuadrada o a la dependencia lineal entre las columnas o filas de la matriz. Es importante entender las consecuencias de esta propiedad para poder abordar correctamente la resolución de sistemas de ecuaciones y comprender sus posibles resultados.

Existen situaciones en las que no tener una matriz inversa puede ser beneficioso

La propiedad de tener una matriz inversa es fundamental en el álgebra lineal. Sin embargo, existen situaciones específicas en las que no contar con la inversa de una matriz puede ser beneficioso y útil para resolver problemas particulares.

Cuando una matriz no tiene una inversa, significa que no podemos encontrar otra matriz que, al multiplicarla por esta matriz original, nos dé como resultado la identidad. Esta situación se presenta cuando la matriz no es cuadrada o cuando su determinante es igual a cero.

1. Matrices no cuadradas

Las matrices no cuadradas son aquellas que tienen diferente número de filas y columnas. Estas matrices no pueden tener una inversa, ya que para que una matriz sea invertible, debe ser cuadrada (es decir, tener el mismo número de filas y columnas).

A pesar de no tener una inversa, las matrices no cuadradas aún se utilizan en numerosos campos de las ciencias y la ingeniería. Por ejemplo, en problemas de ajuste de curvas o en la resolución de sistemas sobredeterminados, donde el número de ecuaciones es mayor que el número de incógnitas.

2. Matrices singulares

Una matriz singular es aquella cuyo determinante es igual a cero. En este caso, tampoco existe una inversa. Las matrices singulares son de gran importancia en diversas áreas, como la teoría de grafos, la investigación de operaciones y el análisis de redes.

Por ejemplo, en la teoría de grafos, podemos utilizar matrices singulares para representar relaciones de dependencia o conexiones entre nodos y aristas. Estas matrices nos permiten estudiar y analizar la estructura de los grafos sin necesidad de invertirlas.

Beneficios de no tener una matriz inversa

Aunque pueda parecer contradictorio, no tener una matriz inversa puede ofrecer ciertos beneficios en determinadas situaciones. Algunos de estos beneficios son:

• Simplificación de cálculos: Al no tener una matriz inversa, podemos evitar realizar operaciones innecesarias y simplificar los cálculos matemáticos durante la resolución de problemas.
• Mayor estabilidad numérica: En algunos algoritmos y métodos numéricos, el hecho de trabajar con matrices no invertibles puede mejorar la estabilidad y precisión de los resultados obtenidos.
• Nuevas perspectivas y enfoques: La ausencia de una inversa nos obliga a buscar soluciones alternativas y explorar diferentes enfoques para resolver un problema dado.

Si bien tener una matriz inversa es una propiedad crucial en el álgebra lineal, existen casos en los que no contar con ella puede ser beneficioso y abrir nuevas posibilidades para el análisis y resolución de problemas. Es importante comprender estas situaciones y utilizarlas adecuadamente en contextos específicos.

Qué alternativas existen cuando una matriz no tiene inversa

Cuando nos encontramos con una matriz que no tiene inversa, es importante conocer las alternativas que existen para trabajar con ella. En este artículo, exploraremos estas alternativas y analizaremos las razones y consecuencias de esta propiedad crucial.

1. Reducción por filas

Una de las alternativas más comunes cuando una matriz no tiene inversa es utilizar la técnica de reducción por filas. Esta técnica implica la transformación de la matriz original en una forma escalonada reducida, lo que nos permite obtener información valiosa sobre el sistema de ecuaciones al que está relacionada.

La reducción por filas proporciona un método efectivo para resolver sistemas de ecuaciones lineales cuando una matriz no tiene inversa. A través de operaciones elementales, como intercambiar filas, multiplicar o sumar filas por un escalar, podemos obtener una solución consistente o inconsistente del sistema.

2. Uso de pseudoinversa

Otra alternativa útil cuando una matriz no tiene inversa es utilizar su pseudoinversa. La pseudoinversa es una generalización de la noción de inversa de una matriz, que se define incluso cuando la matriz no es cuadrada o no es invertible.

La pseudoinversa se utiliza principalmente en problemas de mínimos cuadrados, donde se busca encontrar la "mejor" solución posible a un sistema de ecuaciones sobredeterminado. A través de la pseudoinversa, podemos obtener una solución aproximada que minimiza la diferencia entre los valores predichos y los observados.

3. Descomposición en valores singulares

La descomposición en valores singulares es otra técnica muy utilizada cuando una matriz no tiene inversa. Esta descomposición nos permite descomponer una matriz en tres matrices más simples: una matriz unitaria a la izquierda, una matriz diagonal que contiene los valores singulares y una matriz unitaria a la derecha.

Utilizando esta descomposición, podemos realizar cálculos eficientes y obtener soluciones aproximadas para sistemas de ecuaciones lineales cuando una matriz no es invertible. La descomposición en valores singulares es ampliamente utilizada en aplicaciones como el análisis de componentes principales y la compresión de datos.

4. Utilizar técnicas de aproximación

En algunos casos, cuando una matriz no tiene inversa, se pueden utilizar técnicas de aproximación para obtener soluciones cercanas al sistema deseado. Estas técnicas implican encontrar una matriz "cercana" a la original que sí tenga inversa y que proporcione resultados aceptables para el problema en cuestión.

Existen diferentes enfoques para realizar estas aproximaciones, como la regresión lineal o métodos iterativos como el método de Newton. Cada uno de estos enfoques tiene sus ventajas y desventajas, y la elección dependerá del contexto y los requisitos del problema.

5. Considerar restricciones adicionales

En algunos casos, cuando una matriz no tiene inversa, se pueden introducir restricciones adicionales para restringir las posibles soluciones del sistema de ecuaciones lineales relacionado. Estas restricciones permiten encontrar soluciones factibles dentro del contexto específico del problema.

Las restricciones adicionales pueden ser de diferentes tipos, como restricciones de no negatividad, restricciones de igualdad o restricciones de norma. Al imponer estas restricciones, podemos definir un problema más completo y encontrar soluciones viables incluso cuando la matriz original no es invertible.

Cuando nos encontramos con una matriz que no tiene inversa, existen diversas alternativas que podemos utilizar para abordar el problema. Desde técnicas de reducción por filas hasta el uso de pseudoinversas o descomposiciones en valores singulares, cada enfoque tiene sus ventajas y desventajas. La elección de la mejor alternativa dependerá del contexto y los requisitos específicos del problema en cuestión.

Cómo puedo manejar la falta de una matriz inversa en mis cálculos o análisis matemáticos

La falta de una matriz inversa es un escenario común que puede ocurrir en el ámbito de las matemáticas y tiene importantes implicaciones. Cuando una matriz no tiene inversa, esto significa que no es posible encontrar otra matriz que al multiplicarla por la original resulte en la matriz identidad.

Una de las razones más comunes por las que una matriz no tiene inversa es cuando su determinante es igual a cero. El determinante de una matriz se calcula mediante una fórmula específica que implica sumas y productos de los elementos de la matriz. Si el resultado final es cero, entonces esto indica que la matriz no puede ser invertida.

La ausencia de una matriz inversa tiene importantes consecuencias en diversos campos de estudio. En el álgebra lineal, la existencia de una matriz inversa es crucial para poder resolver sistemas de ecuaciones lineales mediante la técnica de la matriz aumentada. Si una matriz no tiene inversa, entonces el sistema de ecuaciones puede tener múltiples soluciones o incluso ninguna solución. Esto puede complicar significativamente la resolución de problemas y puede requerir el uso de métodos alternativos para obtener una solución factible.

Además, la falta de una matriz inversa también puede impactar en el cálculo de determinantes y la solución de ecuaciones lineales utilizando otros métodos como la regla de Cramer. Estos métodos se basan en propiedades algebraicas de las matrices inversibles, por lo que si una matriz carece de inversa, estos métodos pueden volverse inaplicables o generar resultados incorrectos.

En aplicaciones prácticas como la ingeniería, la física o la computación, encontrarse con una matriz no invertible puede tener consecuencias significativas. Por ejemplo, en el análisis de circuitos eléctricos, una matriz no invertible puede implicar que el sistema de ecuaciones no tiene una solución única y, por lo tanto, la configuración del circuito puede ser problemática o impredecible. En programación, cuando se trabaja con transformaciones de coordenadas o matrices de cambio de base, la falta de una matriz inversa puede llevar a errores en el cálculo de nuevas coordenadas o a resultados inesperados.

Cuando una matriz no tiene inversa, nos encontramos con un desafío matemático importante. Esta propiedad afecta directamente a muchas áreas de estudio y aplicaciones prácticas, complicando el análisis y la resolución de problemas. Es fundamental comprender las razones y consecuencias de la falta de una matriz inversa para poder abordar adecuadamente estos problemas y encontrar soluciones alternativas cuando sea necesario.

¿Cuáles son los casos especiales en los que una matriz pueda tener una pseudo-inversa en lugar de una inversa tradicional?

Cuando hablamos de matrices, uno de los conceptos más importantes es el de la inversa. Una matriz inversa tiene propiedades muy particulares y nos permite resolver ecuaciones lineales de una manera sencilla. Sin embargo, no todas las matrices tienen una inversa.

En algunos casos especiales, una matriz puede tener lo que se conoce como una pseudo-inversa en lugar de una inversa tradicional. La pseudo-inversa es una generalización del concepto de inversa y se utiliza cuando la matriz no cumple las condiciones necesarias para tener una inversa.

Existen varias razones por las cuales una matriz no tiene una inversa. Una de ellas es cuando la matriz no es cuadrada. Recordemos que para que una matriz tenga una inversa, debe ser una matriz cuadrada, es decir, tener el mismo número de filas que de columnas.

Otra razón por la cual una matriz puede no tener una inversa es cuando la determinante de la matriz es igual a cero. La determinante de una matriz es un número que se calcula a partir de sus elementos y es utilizado para determinar si una matriz tiene una inversa o no.

Además, una matriz puede no tener inversa cuando alguna de sus columnas o filas es una combinación lineal de las demás. Esto significa que se puede formar una columna o fila utilizando una combinación de las demás, lo que hace que la matriz sea singular y no tenga una inversa definida.

Es importante destacar que cuando una matriz no tiene una inversa, esto implica ciertas consecuencias en términos de sistemas de ecuaciones lineales. Si tenemos un sistema de ecuaciones representado por una matriz sin inversa, significa que el sistema no tiene una única solución. En lugar de eso, puede tener infinitas soluciones o incluso ninguna solución.

La pseudo-inversa es una herramienta que nos permite lidiar con estos casos especiales. A diferencia de la inversa tradicional, la pseudo-inversa puede calcularse para cualquier tipo de matriz, ya sea cuadrada o rectangular. La pseudo-inversa se utiliza para encontrar soluciones aproximadas en sistemas de ecuaciones sin solución única.

Aunque en la teoría matemática ideal todas las matrices tendrían una inversa, este no siempre es el caso en la práctica. Cuando una matriz no cumple ciertas condiciones, como no ser cuadrada o tener determinante cero, no tendrá una inversa tradicional. Sin embargo, podemos utilizar la pseudo-inversa como una alternativa viable para resolver sistemas de ecuaciones lineales en estas situaciones especiales.

Qué aplicaciones prácticas tiene el conocimiento de las propiedades de las matrices sin inversa

El conocimiento de las propiedades de las matrices sin inversa tiene una amplia gama de aplicaciones prácticas en diversos campos. Estas propiedades pueden ayudarnos a entender mejor los sistemas lineales, la geometría y el álgebra lineal.

Sistemas lineales

En el estudio de los sistemas lineales, las matrices desempeñan un papel fundamental. Cuando una matriz no tiene inversa, significa que existe una combinación lineal de las ecuaciones del sistema que no tiene solución. Esta información es crucial para determinar si un sistema lineal es consistente o inconsistente.

Por ejemplo, al resolver un sistema de ecuaciones lineales usando la eliminación de Gauss-Jordan, si encontramos que una fila entera se convierte en una fila de ceros después de aplicar las operaciones elementales, entonces sabemos que la matriz correspondiente al sistema no tiene inversa y, por lo tanto, el sistema es inconsistente.

Geometría

Las matrices sin inversa también tienen importantes implicaciones en la geometría. Por ejemplo, si una matriz no tiene inversa, significa que las transformaciones lineales asociadas a esa matriz no son biyectivas, es decir, no hay una correspondencia uno a uno entre los puntos de partida y los puntos de llegada.

Esto puede ser útil en el análisis de figuras geométricas y sus transformaciones. Al comprender cuando una matriz no tiene inversa, podemos identificar aquellos casos en los que las dimensiones de una figura se reducen o no cambian al aplicar una transformación lineal, como en la contracción o el colapso hacia un punto específico.

Álgebra lineal

El estudio de las matrices sin inversa también es esencial en el álgebra lineal. Estas matrices, a diferencia de las matrices invertibles, no tienen una matriz inversa que les permita deshacer las operaciones realizadas.

Esta propiedad nos lleva a considerar las matrices singulares y los espacios nulos. Una matriz singular es aquella que no tiene inversa, y el espacio nulo de una matriz está compuesto por todos los vectores que se transforman en el vector cero cuando se multiplican por esta matriz singular.

Este concepto de espacio nulo resulta especialmente útil en el análisis de ecuaciones homogéneas y la resolución de problemas que involucran sistemas de ecuaciones con soluciones triviales o nulas.

Entender las propiedades de las matrices sin inversa nos proporciona valiosas herramientas para analizar sistemas lineales, figuras geométricas y problemas de álgebra lineal. Su aplicación práctica abarca muchos campos, como la ingeniería, la física, la informática y la estadística, siendo crucial para comprender y resolver problemas complejos en estas áreas.

Preguntas frecuentes (FAQ)

1. ¿Qué significa que una matriz no tiene inversa?

Significa que la matriz no puede ser invertida y que no existe otra matriz tal que, al multiplicarla por la matriz original, se obtenga la matriz identidad.

2. ¿Cuáles son las razones por las que una matriz no tiene inversa?

Una matriz no tiene inversa si es singular, es decir, si su determinante es igual a cero.

3. ¿Qué consecuencias tiene que una matriz no tenga inversa?

No se pueden resolver ecuaciones lineales utilizando métodos de inversión de matrices, y el sistema de ecuaciones correspondiente puede no tener una solución única o puede no tener solución.

4. ¿Cómo puedo saber si una matriz tiene inversa?

Si el determinante de la matriz es distinto de cero, entonces la matriz tiene inversa. De lo contrario, no la tiene.

5. ¿Qué puedo hacer si una matriz no tiene inversa y necesito resolver un sistema de ecuaciones lineales?

En lugar de utilizar la inversión de matrices, puedes utilizar otros métodos como eliminación gaussiana, descomposición LU o descomposición QR para resolver el sistema de ecuaciones.