Descubre cuál opción incluye las tres expresiones algebraicas y aumenta tu dominio de matemáticas
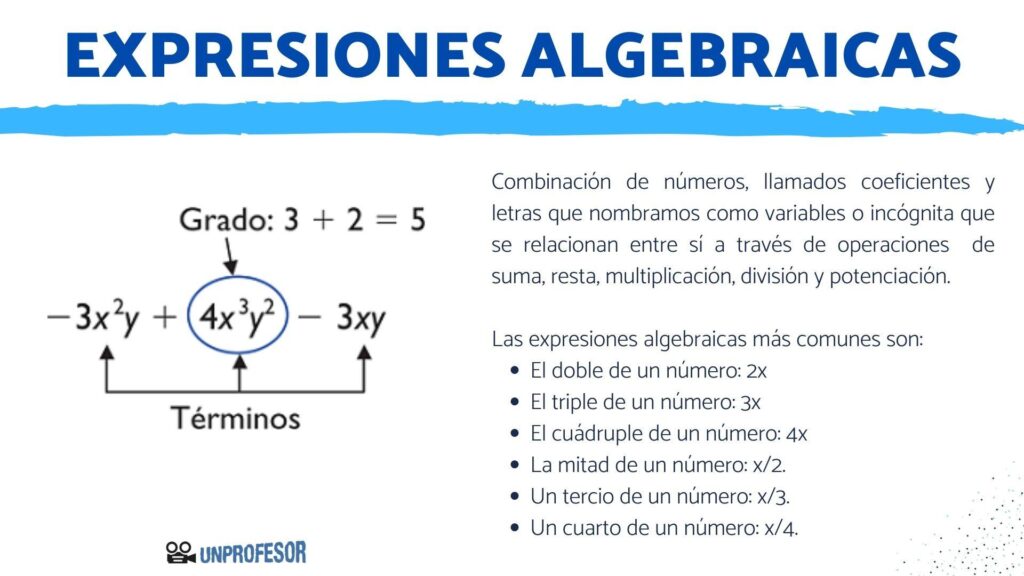
Las expresiones algebraicas son un elemento fundamental en el estudio de las matemáticas. Estas expresiones, formadas por variables y constantes, nos permiten resolver problemas y representar situaciones reales de manera simbólica. Sin embargo, puede resultar difícil reconocer cuál opción incluye las tres expresiones algebraicas correctas.
Te presentaremos algunos ejemplos de expresiones algebraicas y te mostraremos cómo identificar aquellas que son correctas. Además, aprenderás a diferenciar entre una expresión algebraica y un término algebraico, así como a simplificar y evaluar estas expresiones. Aumenta tu dominio de las matemáticas con esta guía sobre expresiones algebraicas.
- Qué son las expresiones algebraicas y por qué son importantes en matemáticas
- Cómo simplificar y expandir expresiones algebraicas para facilitar su análisis
- Cuáles son las diferentes operaciones que se pueden realizar con expresiones algebraicas
- Cómo resolver ecuaciones lineales y cuadráticas utilizando expresiones algebraicas
- Cuál es la importancia de las expresiones algebraicas en la resolución de problemas del mundo real
- Cuáles son algunas estrategias y técnicas útiles para trabajar con expresiones algebraicas de manera eficiente
- Cómo utilizar el álgebra para modelar situaciones y resolver problemas cotidianos
- Cuáles son los errores comunes a evitar al trabajar con expresiones algebraicas
- Cuál es la relación entre las expresiones algebraicas y otras ramas de las matemáticas, como el cálculo y la geometría
- Cómo mejora el dominio de matemáticas el conocimiento y manejo de las expresiones algebraicas
- Preguntas frecuentes (FAQ)
Qué son las expresiones algebraicas y por qué son importantes en matemáticas
Las expresiones algebraicas son combinaciones de números, letras y operaciones matemáticas que nos permiten representar y simplificar problemas en las matemáticas. Son un componente fundamental en el álgebra y se utilizan ampliamente en muchos campos, desde la física hasta la economía.
Una expresión algebraica puede contener variables, coeficientes, exponentes y operaciones como suma, resta, multiplicación y división. Estas expresiones nos permiten describir relaciones entre cantidades desconocidas y resolver ecuaciones.
En matemáticas, el dominio se refiere al conjunto de valores para los cuales una función o expresión es válida. A través del estudio de las expresiones algebraicas, podemos expandir nuestro dominio de matemáticas y adquirir habilidades para resolver problemas más complejos.
Es importante entender las expresiones algebraicas porque nos ayudan a desglosar situaciones complicadas en sus componentes más simples y comprender cómo se relacionan entre sí. Nos permiten manipular y transformar ecuaciones para llegar a soluciones precisas y analizar diferentes escenarios.
Además, las expresiones algebraicas nos brindan una base sólida para la comprensión de conceptos más avanzados en matemáticas, como las funciones lineales y cuadráticas, sistemas de ecuaciones y matrices. También son esenciales para resolver problemas en campos como la ingeniería, la física, la estadística y la economía.
Por lo tanto, si quieres mejorar tu dominio de matemáticas y ser capaz de resolver problemas más desafiantes, es fundamental familiarizarte con las expresiones algebraicas y su aplicación en diversos contextos. A medida que te familiarices con estas expresiones, podrás desarrollar tu capacidad para descomponer problemas en partes más manejables y encontrar soluciones efectivas.
Cómo simplificar y expandir expresiones algebraicas para facilitar su análisis
Las expresiones algebraicas son fundamentales en el estudio de las matemáticas, pero a menudo pueden resultar confusas y complicadas. Sin embargo, existen técnicas que nos permitensimplificaryexpandirestas expresiones, lo cual facilita suanálisis y comprensión**.
¿Qué es simplificar una expresión algebraica?
Simplificar una expresión algebraica implica reducir su forma lo más simple posible, eliminando términos semejantes y realizando operaciones aritméticas básicas. Esto nos ayuda a tener una representación más clara de la expresión y a facilitar su manipulación.
Existen varias reglas y propiedades algebraicas que nos permitensimplificaruna expresión de manera efectiva. Algunas de estas reglas incluyen:
Regla del cero:Si tenemos un término con un coeficiente igual a cero, podemos eliminar ese término de la expresión ya que no afectará el resultado final.Propiedad distributiva:Permitesimplificarexpresiones que contienen productos y sumas o restas. Para aplicar esta propiedad, multiplicamos cada término dentro de los paréntesis por el coeficiente que se encuentra fuera de ellos.Regla de los exponentes:Nos permitesimplificarexpresiones que contienen potencias. Por ejemplo, si tenemos una potencia elevada a otra potencia, podemos multiplicar los exponentes parasimplificarla expresión.
Estas son solo algunas de las reglas que se utilizan parasimplificarexpresiones algebraicas. Es importante tener en cuenta que cada expresión puede requerir un enfoque diferente y es posible que se deban realizar varias simplificaciones secuenciales.
¿Qué es expandir una expresión algebraica?
Expandir una expresión algebraica implica distribuir y multiplicar los términos presentes en la expresión. Esto nos permite ver la expresión original como una suma o resta de términos individuales, lo cual facilita su manipulación y análisis.
La propiedad distributiva es fundamental paraexpandirexpresiones algebraicas. Si tenemos una expresión con paréntesis y multiplicaciones, podemos distribuir el coeficiente hacia cada término dentro de los paréntesis. Luego, realizamos las multiplicaciones necesarias para obtener la formaexpandidade la expresión.
Por ejemplo, si tenemos la expresión (2x + 3)(4y - 5), podemos utilizar la propiedad distributiva paraexpandirla**:
(2x + 3)(4y - 5) = 2x * 4y + 2x *(-5) + 3 * 4y + 3 * (-5)
El resultado de esta operación nos dará la formaexpandidade la expresión original.
Alexpandiruna expresión algebraica, es importante tener en cuenta las reglas de signos y realizar las operaciones aritméticas correspondientes.
Tanto lasimplificacióncomo laexpansiónde expresiones algebraicas son técnicas fundamentales para facilitar el análisis y la comprensión de estas expresiones matemáticas. Mediante el uso adecuado de reglas y propiedades algebraicas, podemossimplificarexpresiones complejas yexpandirlasen términos más simples. Esto nos permite resolver problemas matemáticos con mayor facilidad, así como establecer relaciones y patrones entre diferentes expresiones.
Cuáles son las diferentes operaciones que se pueden realizar con expresiones algebraicas
Las expresiones algebraicas son fundamentales en el estudio de las matemáticas. Con ellas, podemos representar situaciones y problemas de manera simbólica, lo que nos permite realizar operaciones y simplificaciones para llegar a soluciones concretas.
En general, existen tres operaciones básicas que se pueden realizar con expresiones algebraicas: sumar, restar y multiplicar. Estas operaciones nos permiten combinar términos y simplificar nuestras expresiones para obtener resultados más simples y fáciles de trabajar.
Suma de expresiones algebraicas
La suma de expresiones algebraicas consiste en combinar los términos semejantes de dos o más expresiones. Para esto, es importante recordar que solo se pueden sumar aquellos términos que tienen la misma variable elevada a la misma potencia.
Para sumar expresiones algebraicas, simplemente sumamos los coeficientes de los términos semejantes y mantenemos la variable y su exponente sin cambios. Si no hay términos semejantes en las expresiones, simplemente se escriben uno al lado del otro.
Resta de expresiones algebraicas
La resta de expresiones algebraicas es similar a la suma, pero en lugar de sumar los términos, restamos sus coeficientes. Al igual que en la suma, solo podemos restar términos semejantes, es decir, aquellos con la misma variable y exponente.
Al igual que en la suma, si no hay términos semejantes, simplemente escribimos uno al lado del otro y cambiamos el signo de los términos que queremos restar.
Multiplicación de expresiones algebraicas
La multiplicación de expresiones algebraicas consiste en aplicar la propiedad distributiva entre los términos de las expresiones. Para ello, multiplicamos cada término de la primera expresión por cada término de la segunda expresión y luego simplificamos el resultado.
Es importante tener en cuenta que cuando multiplicamos dos términos, multiplicamos sus coeficientes y sumamos los exponentes de las variables. Si hay más de dos términos en cada expresión, repetimos este proceso para todos los posibles pares de términos.
Una vez que hemos realizado todas las multiplicaciones, podemos simplificar la expresión resultante combinando términos semejantes si es necesario.
Saber realizar estas tres operaciones básicas con expresiones algebraicas es fundamental para poder trabajar con eficacia en las matemáticas. Dominar estas operaciones nos permitirá simplificar expresiones, resolver ecuaciones y plantear problemas en forma simbólica, lo que nos brinda una mayor comprensión y dominio de esta disciplina tan importante.
Cómo resolver ecuaciones lineales y cuadráticas utilizando expresiones algebraicas
Las ecuaciones lineales y cuadráticas son fundamentales en el estudio de las matemáticas. Resolver estas ecuaciones es una habilidad esencial que te permitirá comprender y aplicar conceptos más avanzados en álgebra y cálculo. En este artículo, te mostraremos cómo resolver ecuaciones lineales y cuadráticas utilizando expresiones algebraicas, lo cual te ayudará a aumentar tu dominio de las matemáticas.
Resolviendo ecuaciones lineales
- Paso 1: Asegúrate de tener la ecuación en su forma estándar, es decir, con todas las variables en un lado y el término constante en el otro lado.
- Paso 2: Utiliza las propiedades de la igualdad para simplificar la ecuación y despejar la variable que deseas encontrar.
- Paso 3: Simplifica ambos lados de la ecuación hasta llegar a un valor único para la variable.
- Paso 4: Verifica tu solución sustituyendo el valor encontrado en la ecuación original. Si la igualdad se cumple, entonces has resuelto correctamente la ecuación lineal.
Resolviendo ecuaciones cuadráticas
Las ecuaciones cuadráticas tienen la forma ax^2 + bx + c = 0, donde a, b y c son coeficientes y x es la variable que deseamos encontrar. Para resolver estas ecuaciones, podemos utilizar diferentes métodos, como:
- Factorización: Si es posible, factorizamos la ecuación cuadrática para encontrar las raíces.
- Completar el cuadrado: Este método consiste en convertir la ecuación cuadrática a una forma de binomio al cuadrado perfecto y luego despejar la variable.
- Fórmula general: La fórmula general para resolver una ecuación cuadrática es x = (-b ± √(b^2 - 4ac))/(2a), donde ± indica que hay dos posibles soluciones, una sumando y otra restando la raíz cuadrada.
Es importante tener en cuenta que las ecuaciones cuadráticas pueden tener dos soluciones reales y distintas, una solución doble (cuando la raíz es única) o ninguna solución real (cuando el discriminante es negativo).
Resolver ecuaciones lineales y cuadráticas utilizando expresiones algebraicas nos permite desarrollar habilidades fundamentales en matemáticas y aplicarlas en problemas más complejos. Recuerda practicar estos métodos y comprender el razonamiento detrás de cada paso para mejorar tu dominio de las matemáticas.
Cuál es la importancia de las expresiones algebraicas en la resolución de problemas del mundo real
Las expresiones algebraicas son fundamentales en la resolución de problemas del mundo real. A través de ellas, podemos representar situaciones complejas en forma de fórmulas y ecuaciones, lo que nos permite analizarlas, simplificarlas y resolverlas de manera más eficiente.
Una expresión algebraica consiste en la combinación de números, variables y operaciones matemáticas, como sumas, restas, multiplicaciones y divisiones. Estas expresiones pueden incluir tanto términos numéricos como términos con incógnitas, lo que nos brinda la flexibilidad necesaria para trabajar con situaciones variables y desconocidas.
¿Por qué es importante dominar las expresiones algebraicas?
El dominio de las expresiones algebraicas es esencial para tener un buen desempeño en matemáticas y en diversos campos relacionados. A continuación, se presentan algunas razones por las cuales es importante desarrollar este dominio:
- Resolución de problemas: Las expresiones algebraicas nos permiten abordar problemas complejos y encontrar soluciones mediante el uso de ecuaciones y fórmulas. Desde cálculos financieros hasta análisis de datos científicos, el dominio de las expresiones algebraicas es esencial para enfrentar una amplia gama de situaciones.
- Modelado de situaciones: Las expresiones algebraicas nos brindan la capacidad de traducir situaciones del mundo real a un lenguaje matemático. Esto nos permite analizar y comprender fenómenos complejos, como el crecimiento de poblaciones, los cambios en los precios o las trayectorias de objetos en movimiento.
- Generalización y abstracción: El trabajo con expresiones algebraicas nos ayuda a desarrollar habilidades de generalización y abstracción. Al manipular símbolos y variables, podemos identificar patrones, establecer conexiones y formular reglas generales que se aplican a diferentes situaciones.
- Preparación para estudios superiores y carreras profesionales: Las expresiones algebraicas son fundamentales en áreas como la física, la química, la ingeniería y la economía. Dominar estas herramientas matemáticas desde etapas tempranas nos brinda una base sólida para futuros estudios y carreras en campos relacionados.
Las expresiones algebraicas tienen un papel crucial en la resolución de problemas del mundo real y en el desarrollo de habilidades matemáticas y cognitivas. Es importante dedicar tiempo y esfuerzo a comprender y dominar estos conceptos para aumentar nuestro nivel de competencia en matemáticas y estar preparados para enfrentar desafíos tanto académicos como prácticos en diversas áreas.
Cuáles son algunas estrategias y técnicas útiles para trabajar con expresiones algebraicas de manera eficiente
Trabajar con expresiones algebraicas puede resultar desafiante para muchos estudiantes. Sin embargo, existen diversas estrategias y técnicas que pueden ayudarte a manejarlas de manera más eficiente y aumentar tu dominio en matemáticas.
Una forma efectiva de trabajar con expresiones algebraicas es simplificarlas. Esto implica reducir la expresión a su forma más simple al combinar términos semejantes y eliminar aquellos que se cancelen entre sí. Por ejemplo, si tienes la expresión (2x + 3y) + (4x - 2y), puedes simplificarla sumando los términos de x y los términos de y por separado: 2x + 4x = 6x y 3y - 2y = y. El resultado sería 6x + y.
Identificar patrones
Otra estrategia útil es identificar patrones dentro de las expresiones algebraicas. Al familiarizarte con ciertos patrones comunes, puedes agilizar y simplificar tu trabajo. Por ejemplo, la expresión (a + b)^2 se puede expandir como a^2 + 2ab + b^2. Al reconocer este patrón, puedes evitar la necesidad de expandir la expresión completamente.
Usar propiedades algebraicas
Las propiedades algebraicas también pueden ser de gran ayuda al trabajar con expresiones algebraicas. Estas propiedades incluyen la propiedad distributiva, la propiedad conmutativa y la propiedad asociativa, entre otras. Por ejemplo, la propiedad distributiva establece que a(b + c) es igual a ab + ac. Al aplicar esta propiedad, puedes simplificar expresiones y resolver ecuaciones de manera más eficiente.
Aplicar operaciones inversas
Otra técnica útil es aplicar operaciones inversas para deshacer pasos en el proceso de resolución de una expresión algebraica. Por ejemplo, si tienes la expresión 2x + 5 = 15, puedes encontrar el valor de x restando 5 a ambos lados de la ecuación y luego dividiendo por 2. Al aplicar operaciones inversas de manera adecuada, puedes encontrar soluciones más rápidamente.
- Practica con ejercicios
No hay mejor forma de mejorar tus habilidades en el trabajo con expresiones algebraicas que practicando con ejercicios. Resuelve una variedad de problemas diferentes para familiarizarte con los conceptos y técnicas. Puedes buscar ejercicios de práctica en línea o utilizar libros de texto y cuadernos de ejercicios.
- Utiliza recursos educativos
Existen numerosos recursos educativos disponibles en línea que pueden ayudarte a trabajar con expresiones algebraicas de manera más efectiva. Estos incluyen tutoriales en video, cursos en línea y programas interactivos. Aprovecha estos recursos para fortalecer tus conocimientos y mejorar tus habilidades matemáticas.
Ejemplos y explicaciones detalladas
Al estudiar expresiones algebraicas, es útil contar con ejemplos y explicaciones detalladas que te guíen a través del proceso. Busca ejemplos y explicaciones en línea, en libros de texto o consulta con tus profesores. Estas herramientas te brindarán una comprensión más profunda de los conceptos y te ayudarán a abordar problemas más complejos.
Toma notas y organiza tu trabajo
Al trabajar con expresiones algebraicas, es importante tomar notas y organizarte adecuadamente. Apunta las estrategias y técnicas que encuentres útiles, así como cualquier resultado o fórmula relevante. Organiza tus notas de manera
Cómo utilizar el álgebra para modelar situaciones y resolver problemas cotidianos
El álgebra es una herramienta poderosa que nos permite modelar situaciones y resolver problemas cotidianos de manera eficiente. A través de las expresiones algebraicas, podemos representar relaciones matemáticas y tomar decisiones informadas basadas en datos concretos.
En esta sección, exploraremos cómo utilizar el álgebra para resolver problemas del mundo real y aumentar nuestro dominio de las matemáticas. Veremos ejemplos prácticos que te ayudarán a comprender cómo aplicar conceptos algebraicos en diferentes contextos.
Expresiones algebraicas: la clave para entender el lenguaje matemático
Antes de sumergirnos en el mundo de las aplicaciones del álgebra, debemos tener una comprensión sólida de lo que son las expresiones algebraicas. En términos simples, una expresión algebraica es una combinación de constantes, variables y operadores matemáticos.
Por ejemplo, consideremos la expresión algebraica:
2x + 3y - 5z
En esta expresión, x, y y z son variables y 2, 3 y 5 son constantes. Los operadores matemáticos utilizados son la adición y la sustracción.
Las expresiones algebraicas nos permiten describir y analizar relaciones entre cantidades desconocidas. Podemos usarlas para representar situaciones matemáticas, como la distancia recorrida en un viaje en automóvil, el costo total de una compra o la cantidad de dinero ahorrada en un periodo de tiempo.
Ejemplos de aplicaciones del álgebra en problemas cotidianos
Una vez que entendemos las expresiones algebraicas, podemos comenzar a aplicarlas en problemas cotidianos. Veamos algunos ejemplos:
- Problema 1: Cálculo del área de un terreno rectangular
- Problema 2: Cálculo del promedio de calificaciones
- Problema 3: Cálculo del costo total de una compra con descuento
Supongamos que queremos calcular el área de un terreno rectangular. Sabemos que tiene una longitud de l metros y una anchura de w metros. Podemos representar esta situación con la expresión algebraica:
Área = l * w
Al sustituir los valores numéricos de l y w, podemos obtener el área total del terreno.
Imaginemos que somos estudiantes y queremos saber cuál es nuestro promedio de calificaciones en un curso. Tenemos las calificaciones de diferentes exámenes, cada uno con un peso específico. Podemos representar esta situación con la expresión algebraica:
Promedio = (nota_1 * peso_1 + nota_2 * peso_2 + nota_3 * peso_3) / (peso_1 + peso_2 + peso_3)
Aquí, nota_1, nota_2, nota_3 son las calificaciones de los exámenes y peso_1, peso_2, peso_3 son los pesos correspondientes. Al sustituir los valores numéricos, podemos obtener nuestro promedio de calificaciones.
Supongamos que vamos de compras y encontramos un producto con descuento. El precio original es p dólares y el descuento aplicado es del d por ciento. Podemos representar esta situación con la expresión algebraica:
Costo Total = p - (p * d / 100)
Al sustituir los valores numéricos de p y d, podemos calcular el costo total de nuestra compra.
Estos son solo algunos ejemplos de cómo utilizar el álgebra para modelar situaciones y resolver problemas cotidianos. La capacidad de comprender y aplicar conceptos algebraicos nos proporciona una ventaja significativa al abordar desafíos matemáticos y tomar decisiones fundamentadas en nuestra vida diaria.
Cuáles son los errores comunes a evitar al trabajar con expresiones algebraicas
Las expresiones algebraicas son fundamentales en el estudio de las matemáticas. Aunque pueden parecer complicadas al principio, es crucial tener un buen dominio de ellas para poder resolver problemas y ecuaciones de manera efectiva. Sin embargo, hay algunos errores comunes que debemos evitar al trabajar con expresiones algebraicas.
No simplificar las expresiones antes de operar
Uno de los errores más frecuentes es no simplificar las expresiones algebraicas antes de realizar operaciones con ellas. Esto puede llevar a resultados incorrectos o complicar innecesariamente los cálculos. Es importante recordar que se deben combinar términos semejantes y eliminar paréntesis si es posible antes de proceder con las operaciones.
No respetar el orden de las operaciones
Otro error común es no seguir el orden correcto de las operaciones al trabajar con expresiones algebraicas. Es esencial recordar la regla mnemotécnica PEMDAS (Paréntesis, Exponentes, Multiplicación y División de izquierda a derecha, Suma y Resta de izquierda a derecha) para asegurarnos de hacer los cálculos en el orden adecuado. Ignorar este orden puede llevar a resultados incorrectos y confusiones adicionales.
No utilizar los signos adecuados
Es fundamental utilizar los signos adecuados al trabajar con expresiones algebraicas. Un error común es confundir los signos negativos y positivos al simplificar o combinar términos. Debemos prestar atención a los signos y asegurarnos de aplicar correctamente las reglas de suma y resta cuando sea necesario.
Olvidar de aplicar las propiedades y reglas algebraicas
En ocasiones, se cometen errores al olvidar aplicar las propiedades y reglas algebraicas básicas. Deben recordarse estas reglas esenciales, como la ley distributiva, la propiedad conmutativa y asociativa, entre otras. Estas reglas nos permiten simplificar las expresiones y realizar las operaciones de manera más eficiente.
No verificar los resultados obtenidos
Finalmente, otro error común es no verificar los resultados obtenidos al resolver una expresión algebraica. A menudo, estos cálculos son largos y pueden contener varios pasos. Por lo tanto, es importante tomar el tiempo para revisar nuestros cálculos y asegurarnos de que los resultados sean coherentes y correctos.
Trabajar con expresiones algebraicas puede ser desafiante, pero evitando estos errores comunes podemos aumentar nuestro dominio de las matemáticas. Al simplificar las expresiones, seguir el orden de las operaciones, utilizar los signos adecuados, aplicar las reglas y verificar nuestros resultados, estaremos mejor preparados para enfrentar cualquier problema o ecuación algebraica que se nos presente.
Cuál es la relación entre las expresiones algebraicas y otras ramas de las matemáticas, como el cálculo y la geometría
Las expresiones algebraicas son fundamentales en el estudio de las matemáticas, ya que están presentes en numerosas ramas de esta disciplina, incluyendo el cálculo y la geometría. En este artículo, exploraremos la relación entre las expresiones algebraicas y estas dos áreas clave de las matemáticas, y cómo su comprensión puede aumentar tu dominio de las matemáticas en general.
Expresiones algebraicas en el cálculo
En el cálculo, las expresiones algebraicas son esenciales para describir las funciones y entender los conceptos básicos. Las funciones pueden representarse mediante ecuaciones algebraicas, donde se utilizan variables y operaciones matemáticas para expresar relaciones entre diferentes cantidades. Estas ecuaciones pueden ser manipuladas y analizadas para obtener información valiosa sobre el comportamiento de la función.
Por ejemplo, al estudiar la derivada de una función, se utiliza el álgebra para encontrar la tasa de cambio instantánea de dicha función en un punto dado. La derivación se basa en el uso de límites y operaciones algebraicas como la diferencia y cociente entre incrementos infinitesimales de las variables.
De manera similar, en el cálculo integral, las expresiones algebraicas son empleadas para calcular áreas bajo curvas o encontrar el área entre dos funciones. Además, las técnicas de descomposición en fracciones parciales y sustituciones algebraicas son herramientas cruciales para resolver integrales.
Expresiones algebraicas en la geometría
La geometría también está estrechamente relacionada con las expresiones algebraicas, especialmente en el análisis de formas y figuras geométricas. Al utilizar ecuaciones algebraicas, se pueden describir las propiedades y características de estas formas.
Por ejemplo, la ecuación general de una circunferencia es una expresión algebraica que permite representar todos los puntos en un plano que se encuentran a una distancia constante (radio) de un punto dado (centro). A partir de esta ecuación, se pueden obtener información sobre el radio, el centro y las intersecciones con otros objetos geométricos.
Asimismo, al analizar áreas y volúmenes, se utilizan técnicas algebraicas para calcular dimensiones y resolver problemas. La geometría analítica combina herramientas algebraicas con conceptos geométricos para estudiar las propiedades de figuras en un sistema de coordenadas.
Aumenta tu dominio de matemáticas
Al comprender las relaciones entre las expresiones algebraicas, el cálculo y la geometría, podrás aumentar tu dominio de las matemáticas en general. El álgebra es la base fundamental para el estudio de estas ramas, ya que proporciona las herramientas necesarias para manipular y analizar ecuaciones y funciones.
Al dominar las expresiones algebraicas, podrás resolver problemas más complicados en cálculo y geometría, así como en otras áreas de las matemáticas. Además, entender cómo las expresiones algebraicas se relacionan con estas ramas te permitirá tener una visión más completa y profunda de los conceptos matemáticos.
Las expresiones algebraicas son esenciales en el estudio del cálculo y la geometría, y su comprensión te ayudará a mejorar tu dominio de las matemáticas. Aprovecha esta oportunidad para explorar y profundizar tus conocimientos en estas áreas, y descubre cómo las expresiones algebraicas pueden potenciar tu habilidad para resolver problemas matemáticos.
Cómo mejora el dominio de matemáticas el conocimiento y manejo de las expresiones algebraicas
Las expresiones algebraicas son una parte fundamental de las matemáticas, ya que nos permiten representar situaciones y problemas de manera simbólica. Además, el conocimiento y manejo de estas expresiones es esencial para avanzar en el estudio de álgebra y otras ramas de las matemáticas.
Existen diferentes tipos de expresiones algebraicas, desde las más simples hasta las más complejas. Sin embargo, es importante tener en cuenta que todas comparten una característica común: están compuestas por variables, números y operadores matemáticos.
Beneficios de dominar las expresiones algebraicas
El dominio de las expresiones algebraicas tiene numerosos beneficios para el desarrollo de habilidades matemáticas y la resolución de problemas en general. Algunos de estos beneficios son:
- Mayor comprensión de conceptos matemáticos: El estudio de las expresiones algebraicas implica el dominio de conceptos como los términos, coeficientes, exponentes y variables. Estos conceptos son fundamentales en matemáticas y su comprensión profunda permite entender numerosos temas relacionados.
- Capacidad de simplificar y manipular ecuaciones: Las expresiones algebraicas nos ayudan a entender cómo simplificar y manipular ecuaciones. El uso adecuado de estas técnicas permite resolver problemas con mayor facilidad y eficiencia.
- Mejora en el razonamiento lógico: La resolución de problemas algebraicos requiere un razonamiento lógico y analítico. La práctica constante con expresiones algebraicas fortalece estas habilidades y permite desarrollar un pensamiento más estructurado y deductivo.
- Preparación para la resolución de problemas más complejos: El dominio de las expresiones algebraicas sienta las bases para abordar problemas más avanzados en matemáticas, como sistemas de ecuaciones, factorización, funciones y muchos otros conceptos fundamentales.
Recomendaciones para mejorar el dominio de las expresiones algebraicas
Dominar las expresiones algebraicas requiere tiempo, práctica y paciencia. Aquí te dejamos algunas recomendaciones que te serán de utilidad:
- Estudia los conceptos básicos: Antes de abordar expresiones algebraicas más complejas, asegúrate de comprender bien los conceptos básicos, como variables, coeficientes, términos y exponentes. Esta base sólida te ayudará a entender mejor las expresiones más complicadas.
- Practica con ejercicios: La práctica constante es clave para mejorar el dominio de las expresiones algebraicas. Resuelve variedad de ejercicios que te permitan familiarizarte con las diferentes formas de expresiones y técnicas de manipulación.
- Busca recursos adicionales: Utiliza libros, cursos en línea y videos educativos que te brinden una explicación detallada de los conceptos y técnicas relacionadas con expresiones algebraicas.
- Participa en grupos de estudio o tutorías: El aprendizaje colaborativo puede ser muy útil para el dominio de las expresiones algebraicas. Únete a grupos de estudio o busca la ayuda de un tutor que pueda resolver tus dudas y brindarte orientación adicional.
Dominar las expresiones algebraicas es esencial para mejorar el dominio de matemáticas en general. Su comprensión profunda y práctica constante son clave para fortalecer habilidades matemáticas, desarrollar razonamiento lógico y prepararse para abordar problemas más complejos. Sigue estos consejos y verás cómo tu dominio de las expresiones algebraicas se incrementa, ¡y con él, tu éxito en las matemáticas!
Preguntas frecuentes (FAQ)
1. ¿Cómo simplifico una expresión algebraica?
Para simplificar una expresión algebraica, combina los términos semejantes y reduce la expresión al máximo.
2. ¿Cuál es la diferencia entre una ecuación y una expresión algebraica?
Una ecuación es una igualdad que contiene una o más incógnitas, mientras que una expresión algebraica solo tiene coeficientes y variables.
3. ¿Cuáles son las propiedades de las operaciones algebraicas?
Las principales propiedades de las operaciones algebraicas son: conmutativa, asociativa, distributiva y elemento neutro.
4. ¿Qué es una función lineal en álgebra?
Una función lineal es una relación matemática en la cual la variable dependiente es directamente proporcional a la variable independiente, y se representa mediante una ecuación de la forma y = mx + b.
5. ¿Cómo resuelvo ecuaciones con dos incógnitas?
Para resolver ecuaciones con dos incógnitas, necesitas encontrar los valores numéricos que satisfagan ambas ecuaciones simultáneamente. Esto se puede hacer mediante sustitución, eliminación o utilizando matrices.

Deja una respuesta