Descubre cuántas aristas curvas tiene un cono: la clave para entender su geometría tridimensional

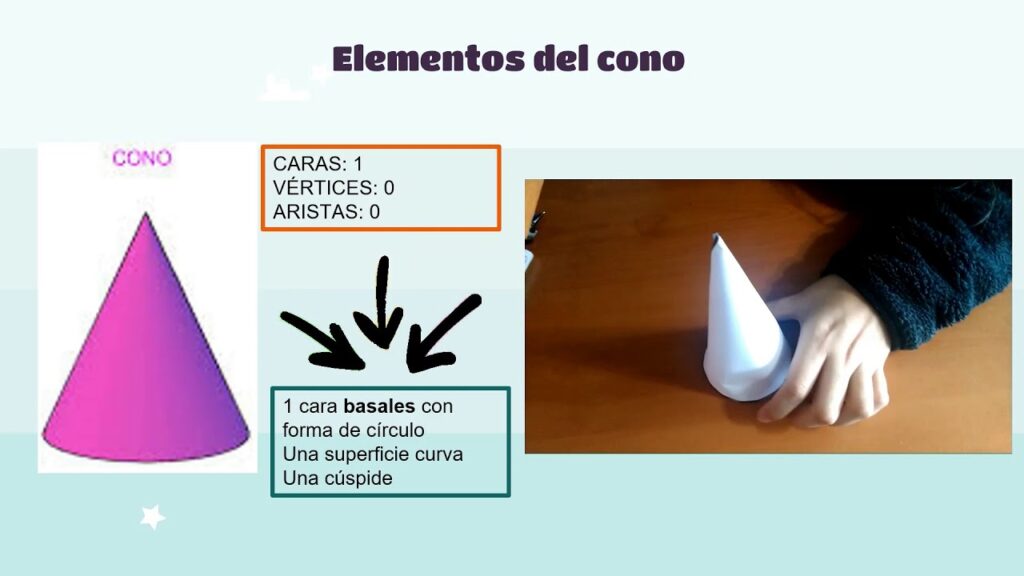
El cono es una figura geométrica tridimensional muy presente en nuestro entorno, desde los helados hasta la forma de muchos objetos cotidianos. Su geometría se caracteriza por tener una base circular y una superficie curva que se va estrechando hacia un vértice puntiagudo. Sin embargo, ¿alguna vez te has preguntado cuántas aristas curvas tiene un cono?

En este artículo exploraremos la respuesta a esta pregunta y analizaremos la importancia de las aristas curvas en la geometría del cono. Veremos cómo estas aristas definen la estructura del cono y cómo afectan su apariencia visual. Además, también revisaremos algunos conceptos básicos de geometría tridimensional para comprender mejor el tema. ¡Sigue leyendo para descubrir más sobre las aristas curvas y sus implicaciones en la geometría del cono!

Cómo se define un cono en geometría tridimensional

Un cono es una figura geométrica tridimensional que se caracteriza por tener una base circular y un vértice puntiagudo llamado ápice. Esta forma cónica es muy común en la naturaleza y se encuentra en una amplia variedad de objetos y estructuras, desde las montañas hasta los helados en forma de cono.

En términos matemáticos, el cono se puede describir como un sólido formado por todos los puntos que están a una distancia constante del ápice y de la base circular. La altura del cono es la distancia entre el ápice y la base, mientras que el radio de la base determina su tamaño.

La geometría tridimensional del cono presenta varias características interesantes. Una de ellas es que tiene una sola arista curva, lo cual lo diferencia de otras figuras como el cilindro o la esfera. Además, el área lateral de un cono está formada por una superficie curva, mientras que el área de la base es plana.

El número de aristas curvas que tiene un cono depende de su forma y dimensiones particulares. En general, un cono recto presenta una única arista curva que une el ápice con cualquier punto de la circunferencia de la base. Esta arista es una curva suave y continua que le confiere al cono su forma característica.

Por otro lado, existen también los conos oblicuos, que son aquellos cuyos ápices no se encuentran en posición vertical sobre la base. Estos conos presentan una arista curva más compleja, ya que su ángulo de inclinación hace que la curva de la arista tenga distintas formas en diferentes secciones.

Es importante destacar que, aunque los conos puedan tener una o varias aristas curvas, siempre conservan sus propiedades fundamentales. Su forma cónica y características geométricas se mantienen sin importar el número de aristas presentes.

Aplicaciones del cono en la vida cotidiana

• Embudos: uno de los usos más comunes del cono es en los embudos, que facilitan el transporte de líquidos o materiales granulados hacia recipientes más pequeños.
• Piramides de helado: los helados servidos en conos son un ejemplo clásico de la geometría del cono. La forma cónica permite que el helado se ajuste perfectamente al cono, evitando derrames.
• Construcción: en arquitectura y construcción, los conos se utilizan para dar forma a torres o chimeneas, brindándoles estabilidad y un aspecto estético agradable.
• Tráfico: los conos de tráfico se utilizan como señalización vial, indicando desvíos, zonas de construcción o situaciones peligrosas en las carreteras.
• Trazado de rutas: los mapas y sistemas de navegación utilizan conos para representar la posición de objetos o puntos de interés en un plano bidimensional.

Cuáles son las características principales de un cono

Un cono es una figura geométrica tridimensional que se caracteriza por tener una base circular y un vértice puntiagudo llamado ápice. Al igual que otros sólidos, el cono también tiene aristas, pero su particularidad radica en que algunas de estas aristas son curvas.

En primer lugar, es importante destacar que un cono está compuesto por una superficie curva llamada lateral o manto del cono, que se extiende desde la base circular hasta el ápice. Esta superficie curva es lo que le confiere al cono esa apariencia tan peculiar y distintiva.

Una característica fundamental de las aristas de un cono es que no todas tienen la misma longitud. En realidad, el cono posee una arista principal conocida como generatriz, que se extiende desde el ápice hasta cualquier punto de la circunferencia de la base. La longitud de esta generatriz depende del tamaño del cono y su inclinación. Mientras más inclinado esté el cono, más larga será la generatriz; mientras que si el cono es más vertical, la generatriz será más corta.

Además de la generatriz, el cono también cuenta con otras aristas importantes, como los segmentos que conectan el ápice con los puntos donde se encuentra la base circular. Estas aristas, llamadas aristas de los vértices, también pueden ser curvas, especialmente si el cono tiene una inclinación significativa.

Todos los conos tienen aristas curvas?

No todos los conos tienen necesariamente aristas curvas. Esta curvatura en las aristas depende de la inclinación del cono. En el caso de los conos rectos, es decir, aquellos en los que el eje del cono forma un ángulo de 90 grados con la base circular, las aristas serán segmentos rectos. Por otro lado, en los conos oblicuos o inclinados, las aristas serán curvas.

Es importante destacar que el número de aristas curvas en un cono puede variar dependiendo de su forma y tamaño. Los conos más esbeltos y afilados tendrán una sola arista curva que corresponderá a la generatriz. Por otro lado, los conos más anchos y menos inclinados tendrán múltiples aristas curvas, incluyendo las aristas de los vértices.

La cantidad de aristas curvas que tiene un cono dependerá de su forma y grado de inclinación. Mientras más inclinado esté el cono, más aristas curvas tendrá. Sin embargo, es importante mencionar que todas las aristas de un cono, ya sean curvas o rectas, son parte importante de su estructura y ayudan a comprender su geometría tridimensional.

Qué es una arista curva y cómo se diferencia de una arista recta

Antes de adentrarnos en el mundo de los conos y sus aristas curvas, es importante entender qué se entiende por una arista curva y cómo se diferencia de una arista recta.

En términos generales, una arista es una línea o segmento donde dos caras de una figura geométrica se encuentran. Estas caras pueden ser planas o curvas, lo que nos lleva a las diferencias entre las aristas curvas y las aristas rectas.

Una arista recta es aquella que se forma cuando dos caras planas o poligonales se encuentran formando un ángulo agudo o recto. Por ejemplo, en un cubo todas las aristas son rectas ya que las caras que lo componen son planas y se encuentran formando ángulos rectos entre sí.

Por otro lado, una arista curva es aquella que nace del encuentro entre dos caras curvas, como sucede en el caso de un cilindro o, más específicamente, en el caso que nos ocupa, un cono. La característica principal de las aristas curvas es su forma suave y redondeada, lo que aporta dinamismo y elegancia a la figura tridimensional.

Es importante tener en cuenta que las aristas curvas no tienen vértices definidos, a diferencia de las aristas rectas que tienen puntos de intersección claros. Las aristas curvas fluyen de manera continua siguiendo la curvatura de las caras que conforman el objeto. Esta propiedad es lo que les da su particularidad y las hace fascinantes de estudiar desde el punto de vista de la geometría tridimensional.

Cuántas aristas curvas tiene un cono

Un cono es una figura geométrica tridimensional que se caracteriza por tener una base circular y un vértice puntiagudo. Es una forma comúnmente encontrada en la naturaleza y en nuestra vida cotidiana, desde los conos de helado hasta los volcanes. Pero ¿alguna vez te has preguntado cuántas aristas curvas tiene un cono?

Para entender el número de aristas curvas de un cono, primero debemos comprender qué es una arista curva. En geometría, una arista es donde dos caras se encuentran, y puede ser curva o recta. En el caso de un cono, las aristas curvas son las líneas que se forman al unir la base circular con el vértice.

La clave está en el desarrollo del cono

Para contar las aristas curvas de un cono, podemos recurrir a su desarrollo, es decir, desplegar la superficie del cono en una lámina plana. Al hacer esto, obtendremos una forma similar a un sector circular, donde el radio de la base del cono corresponde al radio del sector.

Ahora bien, si observamos detenidamente el desarrollo del cono, podremos notar que se forma un contorno circular. Esta circunferencia representa las aristas curvas del cono. Sin embargo, debemos tener en cuenta que esta única circunferencia incluye tanto las aristas curvas como la arista recta que une la base con el vértice.

Entonces, la respuesta a la pregunta de cuántas aristas curvas tiene un cono es sencilla: solo tiene una arista curva. Esta es la línea que recorre la circunferencia del desarrollo del cono y representa la unión entre la base y el vértice.

La importancia de entender las aristas en la geometría tridimensional

Comprender el número y la ubicación de las aristas curvas de un cono es fundamental para comprender su geometría tridimensional. Además de ser una característica distintiva de esta figura, las aristas ayudan a definir su forma y estructura.

Las aristas curvas del cono proporcionan información sobre su simetría y proporciones. Nos permiten visualizar cómo se curva y se estrecha a medida que nos acercamos al vértice. También son útiles para calcular su volumen y área de superficie.

Un cono presenta solo una arista curva, que es la línea circular que une su base con el vértice. Las aristas curvas son una parte integral de la geometría tridimensional y nos ayudan a comprender mejor la forma y estructura de los objetos geométricos.

Espero que este artículo te haya dado una perspectiva clara sobre las aristas curvas de un cono y su importancia en la geometría tridimensional. Ahora podrás admirar no solo la belleza, sino también la complejidad matemática de esta figura versátil.

Cómo se calculan las aristas curvas en un cono

El cálculo de las aristas curvas en un cono es un aspecto fundamental para comprender la geometría tridimensional de esta figura. Las aristas curvas son aquellas líneas que se generan al unir los vértices de la base del cono con el vértice principal, formando una estructura en forma de triángulo curvo.

Para poder determinar cuántas aristas curvas tiene un cono, debemos tener en cuenta sus características principales. Un cono se compone de una base circular y un vértice situado en el centro de dicha base. Las aristas curvas se extienden desde los puntos de la circunferencia de la base hacia el vértice central.

Aplicación de fórmulas geométricas

Para calcular las aristas curvas en un cono, podemos utilizar una serie de fórmulas geométricas que nos permitirán obtener resultados precisos. Una de ellas es la fórmula del perímetro de la base de un cono, que se calcula multiplicando el diámetro por pi (π).

Perímetro = π * Diámetro de la base

Una vez obtenido el perímetro de la base, podremos determinar la longitud de cada una de las aristas curvas. Esto se logra dividiendo el perímetro entre el número de aristas curvas deseadas. Es importante recordar que el número de aristas curvas puede variar dependiendo del nivel de detalle que serequiera en el cálculo.

Otra fórmula útil para el cálculo de las aristas curvas en un cono es la fórmula de la longitud de una circunferencia. Si conocemos el radio de la base del cono, podemos calcular la longitud de cada arista curva utilizando la siguiente fórmula:

Longitud de una arista curva = 2π * Radio de la base

Estas fórmulas nos permiten obtener valores precisos para la longitud de las aristas curvas en un cono. Sin embargo, es importante tener en cuenta que la geometría de los conos puede variar, ya que existen diferentes tipos de conos, como los conos rectos y los conos oblicuos, los cuales presentan diferentes proporciones y ángulos.

Aplicaciones prácticas

El cálculo de las aristas curvas en un cono tiene diversas aplicaciones prácticas en diferentes áreas del conocimiento. En el campo de las matemáticas, el estudio de los conos y sus aristas curvas permite comprender conceptos fundamentales de geometría tridimensional, así como también su relación con otras figuras geométricas.

En la física y la ingeniería, el conocimiento de las aristas curvas en un cono es esencial para el diseño y la construcción de estructuras con forma de cono, como chimeneas industriales, silos o tanques de almacenamiento. El cálculo preciso de las aristas curvas garantiza la estabilidad y resistencia de estas estructuras.

Además, el cálculo de las aristas curvas es útil en campos como la arquitectura, donde se utilizan conos y pirámides para crear diseños atractivos y funcionales. Conocer la cantidad de aristas curvas en un cono permite diseñar formas y estructuras innovadoras que se adapten a las necesidades del proyecto.

El cálculo de las aristas curvas en un cono es un proceso fundamental para comprender su geometría tridimensional. A través de fórmulas geométricas, es posible obtener valores precisos para la longitud de estas aristas, lo que nos permite aplicar este conocimiento en diferentes áreas y disciplinas, como las matemáticas, la física, la ingeniería y la arquitectura. El estudio de los conos y sus aristas curvas nos brinda una visión más completa y profunda del mundo de la geometría tridimensional.

Cuál es la importancia de entender las aristas curvas en la geometría tridimensional del cono

Para comprender completamente la geometría tridimensional de un cono, es fundamental entender el concepto de las aristas curvas. Las aristas curvas son líneas que se forman en la unión entre la base del cono y su vértice, creando una curva continua en todo su perímetro.

La importancia de comprender las aristas curvas radica en su papel clave en la definición y visualización de la forma del cono. Estas aristas no solo definen la estructura y la apariencia del cono, sino que también permiten identificar sus propiedades geométricas específicas.

Al analizar las aristas curvas de un cono, podemos determinar cosas como el grado de inclinación del cono, su altura y su radio. Además, las aristas curvas también influyen en la capacidad del cono para desviar la luz, lo que tiene implicaciones tanto en la óptica como en la acústica.

Cantidad de aristas curvas

Un cono puede tener infinitas aristas curvas, ya que cada punto a lo largo de su base forma una arista curva cuando se conecta con el vértice del cono. Sin embargo, generalmente nos referimos a la cantidad de aristas curvas en relación con el número de divisiones en la base del cono.

Si dividimos la base del cono en n secciones iguales, entonces tendremos n aristas curvas. Cada arista curva sería el segmento de línea que conecta un punto de la base con el vértice. Por lo tanto, cuanto mayor sea el número de secciones o divisiones en la base, mayor será la cantidad de aristas curvas en el cono.

Es importante destacar que las aristas curvas de un cono no son rectas ni forman ángulos fijos. Las aristas siguen una trayectoria curva y cada una está conectada con los vértices vecinos. Esta característica única de las aristas curvas aporta a la figura del cono una forma distintiva y permite su fácil reconocimiento en el espacio tridimensional.

Entender las aristas curvas es fundamental para comprender la geometría tridimensional del cono. Estas aristas definen la forma y las propiedades geométricas del cono, y permiten determinar su inclinación, altura y radio. Además, la cantidad de aristas curvas puede variar según el número de divisiones en la base del cono, lo que le da al cono una apariencia única y reconocible. Así que, la próxima vez que te encuentres con un cono, observa sus aristas curvas y maravíllate ante la belleza y complejidad de la geometría tridimensional.

Existen diferentes tipos de conos con distinta cantidad de aristas curvas

Los conos son uno de los cuerpos geométricos más fascinantes y versátiles que podemos encontrar en el mundo de las matemáticas y la geometría tridimensional. Estos sólidos presentan una forma cónica, con una base circular y una única arista curva que se va ensanchando hacia arriba.

Una de las características más interesantes de los conos es la cantidad de aristas curvas que pueden tener. A diferencia de otros poliedros, como los cubos o las pirámides, que siempre tienen un número fijo de caras y aristas, los conos pueden variar en este aspecto.

Si nos adentramos en el estudio de los conos, descubriremos que existen diferentes tipos que se clasifican según la cantidad de aristas curvas que poseen. En este sentido, tenemos tres categorías principales:

Cono triangular

El cono triangular es el tipo más básico y simple de todos los conos. Se caracteriza por tener una única arista curva, que le confiere su forma característica. Esta arista parte del vértice del cono y recorre su superficie en forma de una curva suave hasta llegar a la base circular. Es importante destacar que el cono triangular carece de aristas rectas adicionales, lo que le otorga una apariencia más suave y redondeada.

Cono cuadrangular

El cono cuadrangular, como su nombre indica, presenta cuatro aristas curvas que parten del vértice y se extienden hasta la base. Estas aristas se distribuyen equidistantemente alrededor del cono, formando un ángulo de 90 grados entre sí. A diferencia del cono triangular, el cono cuadrangular tiene una apariencia más definida y angular debido a la presencia de estas aristas rectas adicionales que se intercalan con las curvas.

Cono poligonal

El cono poligonal es aquel que presenta más de cuatro aristas curvas, lo cual le confiere un aspecto aún más complejo y detallado. En este caso, las aristas parten todas desde el vértice del cono y se distribuyen de manera equidistante alrededor del mismo. La cantidad de aristas curvas dependerá del número de lados que tenga el polígono de la base del cono. Por ejemplo, si la base es un pentágono, el cono poligonal tendrá cinco aristas curvas; si es un hexágono, tendrá seis aristas, y así sucesivamente.

Los conos son cuerpos geométricos que presentan una estructura cónica, con una base circular y una única arista curva que se ensancha hacia arriba. Podemos encontrar diferentes tipos de conos según la cantidad de aristas curvas que posean, siendo los principales el cono triangular, el cono cuadrangular y el cono poligonal. Cada uno de ellos presenta características únicas y distintivas que los hacen especiales dentro del mundo de la geometría tridimensional.

Qué aplicaciones tiene el conocimiento de las aristas curvas en el campo de la arquitectura o el diseño

El conocimiento de las aristas curvas en el campo de la arquitectura y el diseño tiene aplicaciones diversas y muy útiles. Entender cómo se forman y cuántas aristas curvas tiene un cono, por ejemplo, nos permite tener un mayor dominio de la geometría tridimensional y utilizarla de forma eficiente en nuestros proyectos.

En la arquitectura, el uso de aristas curvas puede ser clave para la creación de espacios fluidos y orgánicos que se integren armónicamente con su entorno. Al conocer el número y la forma de estas aristas en un cono, podemos utilizar esta forma geométrica en la creación de techos, cubiertas, fachadas o incluso muros internos, dando lugar a estructuras más innovadoras y estéticamente atractivas.

Además, las aristas curvas también pueden ser de gran utilidad en el diseño de mobiliario y objetos decorativos. Al tener un buen entendimiento de cómo se generan estas aristas en un cono, podemos crear diseños más ergonómicos, suaves y elegantes, que se adapten mejor al cuerpo humano o a las necesidades funcionales específicas de cada objeto.

Por otro lado, es importante destacar que el conocimiento sobre las aristas curvas no solo nos ayuda a crear formas más estéticamente agradables, sino también más eficientes desde el punto de vista estructural. Las aristas curvas pueden distribuir de manera más uniforme las tensiones y cargas en una estructura, lo que puede resultar en un menor consumo de materiales y una reducción de los riesgos de fractura o colapso.

Es importante mencionar que el uso de tecnología de vanguardia, como la impresión 3D o el modelado paramétrico, ha facilitado enormemente la incorporación de aristas curvas en la arquitectura y el diseño. Estas herramientas nos permiten visualizar y analizar de manera precisa las formas generadas por las aristas curvas, así como producir prototipos y estructuras complejas con una mayor eficiencia y precisión.

El conocimiento de las aristas curvas en un cono es fundamental en la arquitectura y el diseño, ya que nos permite explorar nuevas posibilidades creativas, mejorar la funcionalidad de los espacios y objetos diseñados, así como optimizar la eficiencia estructural. Su implementación en proyectos arquitectónicos y de diseño puede generar resultados impactantes y sorprendentes, convirtiendo lo ordinario en extraordinario.

Por qué es relevante estudiar la geometría tridimensional de los conos en áreas como la ingeniería o las ciencias naturales

La geometría tridimensional es una rama fundamental en áreas como la ingeniería, la arquitectura y las ciencias naturales, ya que nos permite comprender y analizar objetos y estructuras en un espacio tridimensional. En particular, el estudio de los conos en geometría tridimensional es de gran relevancia debido a su presencia en numerosas aplicaciones prácticas.

Uno de los aspectos más fascinantes de los conos es su forma característica, que se distingue por tener una base circular y una sola cara curva que se extiende desde la base hasta el vértice. Esta peculiar estructura hace que los conos sean extremadamente útiles en diversas áreas.

En ingeniería, por ejemplo, los conos se utilizan ampliamente en la construcción de materiales, especialmente en la fabricación de recipientes o contenedores cónicos. La forma cónica de estos recipientes permite que los materiales fluyan de manera eficiente y uniforme, lo cual es especialmente importante en procesos industriales como el transporte de líquidos o alimentos a granel. Además, los conos también se emplean en la construcción de chimeneas y torres, donde su forma ayuda a mejorar la dispersión de gases y a garantizar la estabilidad estructural.

En las ciencias naturales, la geometría tridimensional de los conos es esencial para comprender fenómenos físicos y biológicos. Por ejemplo, en física, los conos son relevantes en la teoría de campos, donde representan regiones de influencia de las fuerzas o campos de partículas. Asimismo, en biología, se ha observado que ciertas estructuras de los organismos vivos, como las conchas de algunos moluscos o los pétalos de las flores, siguen patrones cónicos. El estudio de estas formas ayuda a comprender cómo se desarrollan y evolucionan los seres vivos.

El estudio de la geometría tridimensional de los conos es crucial en diferentes campos de aplicación, desde la ingeniería hasta las ciencias naturales. Su forma característica y su capacidad para eficientizar procesos hacen de los conos una herramienta invaluable en numerosas industrias y áreas de investigación. Por tanto, comprender las aristas curvas de los conos es esencial para entender su geometría tridimensional y aplicarla de manera adecuada en diversas situaciones prácticas.

Cuáles son algunos ejemplos prácticos en los que podemos ver la presencia de los conos y sus aristas curvas en nuestra vida diaria

Los conos son una figura geométrica tridimensional que se caracteriza por tener una base circular y una superficie lateral curva que termina en un solo punto, conocido como el vértice. Su forma cónica puede encontrarse en numerosos objetos de nuestro entorno cotidiano.

Uno de los ejemplos más obvios y comunes es el helado. La clásica bola de helado que se coloca sobre un cucurucho tiene la forma de un cono. Además, al observar detenidamente la superficie del helado, podemos apreciar las aristas curvas que le dan su característico aspecto.

Otro ejemplo muy conocido son los volcanes. Los volcanes activos o inactivos tienen una estructura cónica en su parte superior, la cual se forma debido a los materiales expulsados durante las erupciones volcánicas. Estas erupciones generan montañas cónicas con aristas curvas pronunciadas.

En el ámbito de la cocina, también podemos encontrar conos en moldes para realizar cornetas de hojaldre o conos de papel para rellenarlos con crema o algún otro tipo de exquisitez dulce. Estos conos pueden ser utilizados para presentar postres de forma creativa y original.

Además, en el mundo de la construcción, los conos también hacen presencia. Algunas chimeneas pueden tener una forma parecida a la de un cono, con una base circular y una superficie curva. Esto les permite facilitar la salida de humo y gases hacia el exterior de manera eficiente.

Por último, otro ejemplo que es muy popular son los conos de tráfico. Estos conos naranjas, que se utilizan principalmente en las calles y carreteras para delimitar áreas de trabajo o peligro, tienen una forma cónica que les permite ser fácilmente visibles y se mantienen estables gracias a su base ancha.

Aunque a simple vista no nos demos cuenta, los conos y sus aristas curvas están presentes en numerosos ejemplos prácticos de nuestra vida diaria. Ya sea en el helado que disfrutamos en verano, en los volcanes que estudiamos en geografía o incluso en los conos de tráfico que vemos a diario en nuestras calles. La geometría tridimensional de los conos es fundamental para comprender y apreciar la belleza y utilidad de estas figuras geométricas.

Preguntas frecuentes (FAQ)

¿Qué es un cono en geometría?

Un cono es una figura geométrica en tres dimensiones con una base circular y una punta o vértice.

¿Cuántas aristas curvas tiene un cono?

Un cono tiene una única arista curva, que es su borde lateral.

¿Cuántos vértices tiene un cono?

Un cono tiene un único vértice en la punta de la figura.

¿Cuántas caras tiene un cono?

Un cono tiene dos caras: una base circular y una superficie curva que conecta la base con el vértice.

¿Cuáles son las fórmulas para calcular el área y el volumen de un cono?

El área de la base del cono se calcula como A = πr^2, donde r es el radio de la base. El área lateral del cono se calcula como Al = πrl, donde l es la generatriz (la longitud del borde lateral). El volumen del cono se calcula como V = (1/3)πr^2h, donde h es la altura del cono.