Descubre los fascinantes ejes de simetría de esta figura y amplía tu conocimiento sobre geometría

La simetría es un concepto fundamental en la geometría que se encuentra presente en muchos objetos y figuras que nos rodean. Es una cualidad que nos permite encontrar equilibrio y armonía en el mundo que nos rodea, y también es una herramienta importante en campos como el diseño y la arquitectura.

En este artículo exploraremos los ejes de simetría en las figuras geométricas y cómo identificarlos en diferentes casos. Veremos ejemplos de simetría axial y simetría radial, así como algunas propiedades interesantes asociadas a ellos. Además, aprenderemos las características y usos de los ejes de simetría en el arte y la naturaleza. Sumérgete en el fascinante mundo de la simetría y amplía tu conocimiento sobre geometría en este emocionante recorrido.

Qué es un eje de simetría y por qué es importante en geometría

Un eje de simetría es una línea imaginaria que divide una figura en dos partes idénticas. Es decir, si trazamos el eje de simetría, al doblar la figura a lo largo de esa línea, ambas mitades coincidirán perfectamente.

La simetría es un concepto fundamental en geometría, ya que nos permite analizar y comprender la estructura y propiedades de las figuras. A través de los ejes de simetría, podemos identificar patrones y regularidades en diferentes formas geométricas.

Cuando una figura tiene más de un eje de simetría, se conoce como figura simétrica. Las figuras simétricas se encuentran en numerosos contextos, desde la naturaleza hasta el diseño arquitectónico. Al estudiar los ejes de simetría de estas figuras, podemos apreciar su belleza y orden intrínseco.

Tipos de ejes de simetría

Existen diferentes tipos de ejes de simetría según la orientación y cantidad de líneas que los definen:

• Eje de simetría vertical: Este tipo de eje divide la figura en dos partes iguales, una a cada lado del eje. Un ejemplo común de figura con eje de simetría vertical es una figura humana.
• Eje de simetría horizontal: Este tipo de eje divide la figura en dos partes iguales, una encima y otra debajo del eje. Un ejemplo de figura con eje de simetría horizontal es un rectángulo.
• Eje de simetría diagonal: Este tipo de eje divide la figura en dos partes iguales, una a cada lado del eje y con una inclinación diagonal. Un ejemplo de figura con eje de simetría diagonal es un rombo.

Además de estos ejes básicos, también existen figuras con múltiples ejes de simetría, como los polígonos regulares. En un polígono regular, todos los lados y ángulos son iguales, lo que resulta en múltiples ejes de simetría.

Los ejes de simetría no solo se aplican a figuras bidimensionales, sino que también pueden encontrarse en figuras tridimensionales. Por ejemplo, un cubo tiene múltiples ejes de simetría que dividen las caras y las diagonales, mostrando su regularidad y equilibrio en el espacio.

Usos de los ejes de simetría en la vida cotidiana

La simetría y los ejes de simetría tienen aplicaciones prácticas en diversas áreas de la vida cotidiana. Algunos ejemplos incluyen:

• Diseño de logotipos y marcas: Muchas empresas utilizan la simetría y los ejes de simetría en sus logotipos debido a su atractivo visual y sensación de equilibrio.
• Artes visuales: Los artistas utilizan la simetría y los ejes de simetría para crear composiciones armónicas y equilibradas en pinturas, fotografías y esculturas.
• Arquitectura: Los arquitectos utilizan los ejes de simetría para diseñar edificios y estructuras que transmitan una sensación de estabilidad y belleza.
• Biología: En el campo de la biología, la simetría bilateral en los organismos vivos es fundamental para su funcionamiento y desarrollo.

Los ejes de simetría son elementos clave en la geometría que nos permiten analizar y comprender las figuras desde una perspectiva estructural. Su estudio nos ayuda a apreciar la belleza y regularidad presentes en el mundo que nos rodea, además de tener aplicaciones prácticas en diversos campos.

Cuántos ejes de simetría tiene un círculo

El círculo es una figura geométrica que no presenta ejes de simetría. Esto se debe a que un eje de simetría es una línea imaginaria que divide una figura en partes exactamente iguales al reflejarla sobre sí misma.

En el caso del círculo, podemos observar que cualquier línea que pase por su centro lo divide en dos partes, pero no son simétricas entre sí. Si trazamos una línea imaginaria desde el centro de un círculo hasta cualquier punto de su circunferencia, notaremos que las dos partes resultantes no son idénticas ya que una será la parte interior y otra la parte exterior del círculo.

Esta falta de ejes de simetría en el círculo lo diferencia de otras figuras como el cuadrado, el rectángulo o el triángulo, que presentan líneas divisorias que dividen sus partes en regiones simétricas.

Ejes de simetría en otras figuras geométricas

Para comprender mejor qué son los ejes de simetría, es importante mencionar cómo se aplican en otros polígonos regulares.

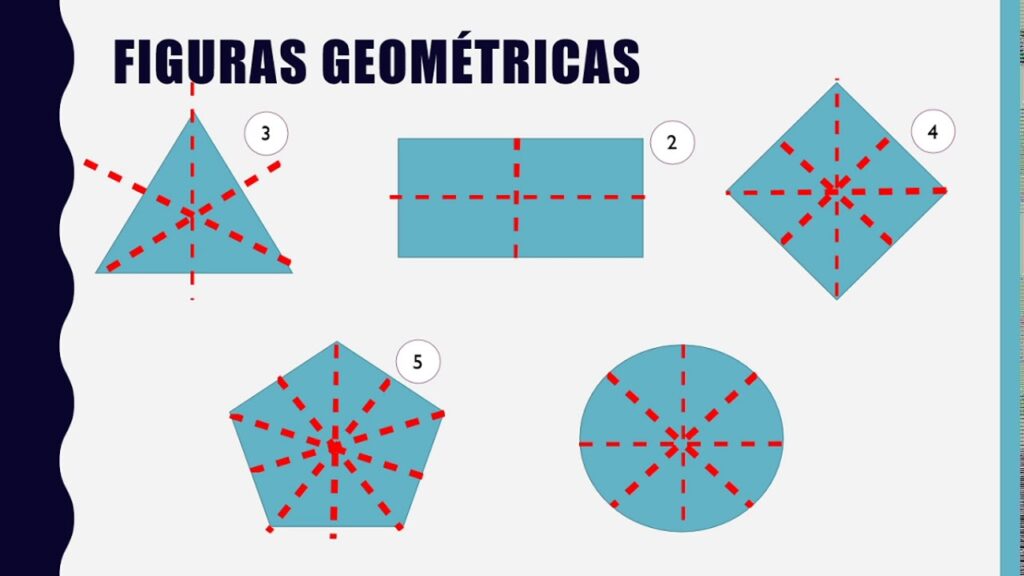
Por ejemplo, un cuadrado tiene cuatro ejes de simetría, ya que cuenta con cuatro lados iguales y cuatro ángulos rectos. Podemos trazar líneas imaginarias a través de su centro y los puntos medios de sus lados para obtener las divisiones simétricas.

Del mismo modo, un rectángulo también posee dos ejes de simetría, que se pueden trazar desde su centro hacia los puntos medios de los lados opuestos más cortos.

En cuanto al triángulo equilátero, cuenta con tres ejes de simetría, los cuales pueden dibujarse desde su centro hasta los vértices y dividen la figura en tres partes iguales.

Este concepto también se aplica a figuras más complejas como el hexágono, octógono, etc., donde podemos contar una cantidad determinada de ejes de simetría según la forma del polígono.

Importancia de los ejes de simetría

Los ejes de simetría son fundamentales en geometría, ya que nos permiten identificar y clasificar diferentes figuras según sus propiedades simétricas. Además de ser útiles en cálculos matemáticos, su estudio también se aplica en otras disciplinas como la arquitectura, el diseño gráfico y la biología.

La simetría es un principio estético muy valorado en diversas áreas, ya que se considera agradable a la vista y genera una sensación de equilibrio y armonía. El conocimiento y comprensión de los ejes de simetría nos permite analizar estructuras y objetos de manera más precisa, lo cual es esencial para el desarrollo de nuevas formas y diseños.

El círculo no presenta ejes de simetría debido a su forma particular, pero otras figuras geométricas como el cuadrado, el rectángulo y el triángulo sí los poseen. Estos ejes ayudan a dividir las figuras en partes idénticas al reflejarlas sobre sí mismas, lo que es fundamental tanto en la geometría como en diferentes disciplinas artísticas y científicas.

Cómo identificar los ejes de simetría en una figura geométrica

Los ejes de simetría de una figura geométrica son líneas imaginarias que dividen la figura en dos partes idénticas. Identificar estos ejes es fundamental para comprender las propiedades y características de diferentes figuras, así como para resolver problemas de geometría.

Existen diferentes maneras de identificar los ejes de simetría en una figura geométrica, dependiendo del tipo de figura y sus propiedades particulares. A continuación, te proporcionaré algunas pautas generales para facilitar este proceso.

1. Observa la forma de la figura

Lo primero que debes hacer es examinar detenidamente la forma de la figura. Busca cualquier simetría visual o patrones repetidos. Si la figura parece ser simétrica con respecto a una línea o eje imaginario, probablemente ese sea uno de los ejes de simetría.

2. Prueba con líneas verticales y horizontales

En muchos casos, las figuras geométricas tienen ejes de simetría verticales u horizontales. Intenta dibujar una línea vertical imaginaria en el centro de la figura y observa si las mitades derecha e izquierda son iguales. Haz lo mismo con una línea horizontal en el medio de la figura. Si ambas mitades son idénticas, has encontrado un eje de simetría.

3. Analiza los ángulos y lados

Otra estrategia útil es estudiar los ángulos y lados de la figura. Si encuentras que los ángulos opuestos son iguales o que los lados correspondientes son iguales en longitud, es probable que haya ejes de simetría presentes.

4. Utiliza la reflexión

La reflexión es una herramienta poderosa para identificar ejes de simetría. Si puedes reflejar la figura en un espejo o en un papel, y la imagen reflejada coincide completamente con la figura original, significa que existe al menos un eje de simetría.

5. Recuerda las características de figuras específicas

Algunas figuras geométricas tienen propiedades particulares en cuanto a sus ejes de simetría. Por ejemplo, un círculo tiene infinitos ejes de simetría, ya que cualquier línea que pase por su centro puede dividirlo en dos partes iguales. Un cuadrado, por otro lado, tiene cuatro ejes de simetría: dos verticales, uno horizontal y uno diagonal.

Identificar los ejes de simetría en una figura geométrica requiere una observación detallada de la forma, el uso de líneas imaginarias, el análisis de ángulos y lados, y la aplicación de la reflexión. Estas habilidades son fundamentales para ampliar tu conocimiento sobre geometría y comprender mejor las propiedades de diferentes figuras.

Cuáles son las propiedades de un triángulo equilátero en cuanto a sus ejes de simetría

Uno de los conceptos fundamentales en geometría es el de los ejes de simetría. Estos ejes son líneas rectas imaginarias que dividen una figura en dos partes iguales y simétricas. En el caso de un triángulo equilátero, existe una serie de propiedades que caracterizan a sus ejes de simetría.

Un triángulo equilátero es aquella figura geométrica que posee sus tres lados de igual longitud y sus tres ángulos internos también iguales, todos ellos de 60 grados. Esto implica que todas las alturas, medianas y bisectrices del triángulo son coincidentes.

En cuanto a los ejes de simetría de un triángulo equilátero, existen tres principales: uno que pasa por su baricentro (el punto de intersección de las medianas), otro que lo atraviesa entre su vértice y su punto medio de la base, y finalmente uno que se encuentra en el medio de cada lado.

Eje de simetría que pasa por el baricentro

El primer eje de simetría de un triángulo equilátero pasa por su baricentro, que es el punto donde se cortan las tres medianas. Esta línea recta divide al triángulo en dos mitades exactamente iguales. Podemos visualizar este eje como si colocáramos un espejo a lo largo de esta línea y obtendríamos una imagen especular reflejada.

Eje de simetría que se encuentra entre el vértice y el punto medio de la base

El segundo eje de simetría es aquel que se extiende desde el vértice del triángulo equilátero hasta el punto medio de la base. Al igual que con el eje anterior, podemos visualizar este eje como si colocáramos un espejo a lo largo de esta línea y obtendríamos una imagen especular reflejada.

Ejes de simetría que se encuentran en el medio de cada lado

Por último, los ejes de simetría que se localizan en el medio de cada lado dividen al triángulo equilátero en dos partes iguales y simétricas. Si colocáramos espejos a lo largo de estas líneas, también obtendríamos imágenes especulares reflejadas.

Un triángulo equilátero tiene tres ejes principales de simetría: uno que pasa por su baricentro, otro que se encuentra entre su vértice y el punto medio de la base, y finalmente uno en el medio de cada lado. Estos ejes dividen al triángulo en partes iguales y simétricas, proporcionando interesantes propiedades geométricas.

Qué tipos de figuras no tienen ejes de simetría

En el mundo de la geometría, existen diversos tipos de figuras que pueden tener ejes de simetría y otras que no. Un eje de simetría es una línea imaginaria que divide a una figura en dos partes iguales y reflectantes entre sí. Esto significa que si pudiéramos colocar un espejo a lo largo de ese eje, la figura se vería reflejada de manera idéntica en ambos lados.

Sin embargo, no todas las figuras tienen ejes de simetría. Algunas figuras son tan asimétricas que no pueden ser divididas en dos partes iguales mediante ninguna línea recta. Estas figuras desafiantes y sin ejes de simetría son fascinantes por su singularidad y complejidad.

Figuras irregulares

Las figuras irregulares son quizás las más conocidas por su falta de simetría. Estas figuras presentan bordes y ángulos completamente distintos entre sí, lo que hace imposible encontrar una línea recta que divida a la figura en dos partes iguales. Ejemplos de figuras irregulares podrían ser una nube, una hoja de árbol o una piedra.

Polígonos regulares

A diferencia de las figuras irregulares, los polígonos regulares son figuras con lados y ángulos iguales. Sin embargo, aunque parecieran tener potencial para tener ejes de simetría, esto no siempre es el caso. Los polígonos regulares solo tienen ejes de simetría si tienen un número par de lados, como el cuadrado, el hexágono regular o el octágono regular. En cambio, los polígonos regulares con un número impar de lados, como el triángulo equilátero o el pentágono regular, no tienen ejes de simetría.

Curvas y formas orgánicas

Las curvas y las formas orgánicas son inherentemente asimétricas debido a su naturaleza fluida y sinuosa. Estas figuras se encuentran en la naturaleza, como las olas del mar, los montones de arena y las estructuras biológicas. Estas figuras no pueden ser divididas en partes iguales mediante una línea recta debido a sus formas complejas y cambiantes.

Otras figuras especiales

Existen otros tipos de figuras que también carecen de ejes de simetría. Por ejemplo, las letras del alfabeto y los números son figuras que, en su mayoría, no poseen ejes de simetría. Aunque algunas letras, como la E, poseen un eje vertical de simetría, la mayoría presenta una combinación de curvas y líneas que hacen que carezcan de simetría en general.

Hay diversos tipos de figuras que no tienen ejes de simetría. Desde figuras irregulares hasta polígonos regulares con un número impar de lados, pasando por curvas y figuras orgánicas, todas ellas presentan una ausencia de simetría que las hace únicas y dignas de estudio. Comprender la falta de simetría en estas figuras nos permite apreciar aún más la belleza y complejidad de la geometría en todas sus formas.

Cómo se pueden utilizar los ejes de simetría en el diseño de objetos y arquitectura

Los ejes de simetría son una herramienta fundamental en el diseño de objetos y arquitectura. Estos ejes proporcionan equilibrio y armonía visual, permitiendo la creación de estructuras estéticamente agradables y funcionales. En este artículo exploraremos cómo se pueden utilizar los ejes de simetría para crear diseños impactantes y ampliar nuestro conocimiento sobre geometría.

En primer lugar, es importante comprender qué es un eje de simetría. Un eje de simetría es una línea imaginaria que divide una figura en dos partes idénticas. Es como si colocáramos un espejo a lo largo de esa línea y la figura reflejada en el espejo sería igual a la figura original. Este concepto se basa en la propiedad de simetría que tienen muchos objetos naturales y artificiales.

Aplicación de los ejes de simetría en el diseño de objetos

En el diseño de objetos, los ejes de simetría desempeñan un papel crucial. Permiten crear piezas con una apariencia equilibrada y armoniosa. Por ejemplo, al diseñar muebles, los diseñadores a menudo utilizan la simetría para asegurarse de que los elementos se vean balanceados. Un sofá con un respaldo simétrico o una mesa con patas también simétricas transmiten una sensación de orden y estabilidad.

Además de añadir equilibrio visual, los ejes de simetría también pueden ayudar en la funcionalidad de los objetos. Por ejemplo, en el diseño de automóviles, las puertas suelen tener ejes de simetría que permiten una apertura y cierre fácil. Del mismo modo, en la creación de utensilios de cocina como tazas o platos, se utiliza la simetría para asegurar un uso cómodo y práctico.

Utilización de los ejes de simetría en la arquitectura

En la arquitectura, los ejes de simetría son fundamentales para crear edificios estéticamente agradables. En muchos estilos arquitectónicos, como el neoclásico o el renacentista, se utilizan ejes de simetría tanto horizontales como verticales para generar un efecto de equilibrio visual. Esto se logra al colocar elementos arquitectónicos, como ventanas, puertas o columnas, de manera simétrica a ambos lados de un eje central.

Los ejes de simetría también pueden ayudar a enfatizar puntos de interés en un edificio. Por ejemplo, en los grandes palacios o catedrales, es común encontrar una entrada principal con una puerta central flanqueada por columnas simétricas. Esta simetría resalta la importancia de esa entrada y guía la mirada hacia ella.

Los ejes de simetría desempeñan un papel crucial en el diseño de objetos y arquitectura. Su aplicación permite crear diseños visualmente equilibrados y funcionales. Ya sea en la creación de muebles, utensilios de cocina o en el diseño de edificios, la comprensión y utilización de los ejes de simetría es fundamental para ampliar nuestro conocimiento sobre geometría y mejorar nuestras habilidades de diseño.

Existen figuras con infinitos ejes de simetría

La simetría es un concepto fundamental en la geometría, y una de las propiedades más interesantes de las figuras geométricas es su capacidad de tener ejes de simetría. Un eje de simetría es una línea imaginaria que divide a una figura en dos partes idénticas o especulares.

En algunas figuras geométricas, como los cuadrados o los círculos, es fácil identificar los ejes de simetría, ya que son evidentes y se pueden trazar rápidamente. Sin embargo, existen figuras que poseen una característica sorprendente: tienen infinitos ejes de simetría.

Las figuras con infinitos ejes de simetría

Hay varios tipos de figuras que cuentan con esta propiedad fascinante. Una de ellas es el pentágono regular, que tiene cinco lados iguales y cinco ángulos iguales. Si trazamos una línea desde un vértice hasta el punto medio del lado opuesto, obtenemos un eje de simetría. Pero si trazamos una línea desde otro vértice hasta cualquier punto del lado opuesto, también obtendremos un eje de simetría.

Otra figura que posee infinitos ejes de simetría es el hexágono regular, aquel que tiene seis lados y seis ángulos iguales. En este caso, al igual que en el pentágono regular, podemos trazar una línea desde un vértice hasta cualquier punto del lado opuesto y obtendremos un nuevo eje de simetría. Cuantas más líneas tracemos, más ejes de simetría aparecerán.

El último ejemplo que mencionaré es el octógono regular, formado por ocho lados iguales y ocho ángulos iguales. Si trazamos una línea desde un vértice hasta cualquier punto del lado opuesto, obtendremos un eje de simetría. Al igual que en los ejemplos anteriores, podemos trazar infinitas líneas y obtener infinitos ejes de simetría.

Estas figuras con infinitos ejes de simetría son tan fascinantes debido a su estructura interna y a la relación entre sus lados y ángulos. Además, demuestran la riqueza y diversidad que se puede encontrar en las diferentes formas geométricas.

Para concluir, es importante destacar que la simetría es un tema apasionante dentro de la geometría y que existen figuras con propiedades sorprendentes, como los ejes de simetría infinitos. Estas figuras nos invitan a explorar más allá de lo evidente y a ampliar nuestro conocimiento sobre geometría, descubriendo nuevas formas y patrones que nos rodean en el mundo.

Qué relación hay entre los ejes de simetría y la reflexión en geometría

En el fascinante mundo de la geometría, los ejes de simetría y la reflexión están estrechamente relacionados. Los ejes de simetría son líneas imaginarias que dividen una figura en dos partes, de modo que cada parte sea una imagen especular de la otra. Por otro lado, la reflexión es una transformación geométrica que produce una copia inversa de una figura a través de un eje de simetría.

Los ejes de simetría pueden encontrarse en diferentes figuras geométricas, desde simples formas como el círculo y el cuadrado hasta estructuras más complejas como polígonos irregulares o figuras tridimensionales. Cada figura puede tener uno o varios ejes de simetría, lo cual influirá en el número de imágenes especulares que se pueden generar mediante la reflexión.

Cómo identificar los ejes de simetría

Identificar los ejes de simetría de una figura puede ser una tarea emocionante y desafiante al mismo tiempo. Existen diferentes métodos para determinar los ejes de simetría dependiendo de la forma de la figura:

• Para figuras con lados rectos, como los cuadrados, rectángulos o trapecios, los ejes de simetría son las líneas que pasan por el centro de los lados opuestos.
• En el caso de los triángulos, los ejes de simetría pueden ser los segmentos que unen los puntos medios de dos lados opuestos o las bisectrices de los ángulos.
• En figuras curvas como el círculo o la elipse, todos los diámetros son ejes de simetría.

Estos son solo algunos ejemplos, pero cada figura presenta sus propias características y reglas para identificar sus ejes de simetría. A medida que te adentres en el fascinante mundo de la geometría, descubrirás que existen patrones y propiedades interesantes relacionados con los ejes de simetría.

Aplicaciones de los ejes de simetría

Los ejes de simetría no solo son una característica estética de las figuras geométricas, sino que también tienen aplicaciones prácticas en diferentes campos:

• En arquitectura y diseño, los ejes de simetría se utilizan para crear edificios o estructuras visualmente equilibradas y armónicas.
• En arte, los artistas utilizan los ejes de simetría como una herramienta para componer sus obras o crear efectos visuales impactantes.
• En biología, los ejes de simetría son fundamentales en el estudio de la morfología y evolución de los seres vivos.
• En matemáticas, los ejes de simetría son un concepto clave en el estudio de las transformaciones geométricas y la simetría.

Estas son solo algunas de las aplicaciones de los ejes de simetría, pero su importancia se extiende a diversos ámbitos de nuestra vida diaria.

Los ejes de simetría y la reflexión en geometría son elementos inseparables que permiten explorar y comprender las propiedades de las figuras desde un enfoque visual y conceptual. A través de su estudio, podemos apreciar la belleza y elegancia de la simetría presente en nuestro entorno, así como ampliar nuestro conocimiento sobre este fascinante campo de las matemáticas.

Cuál es la diferencia entre un eje de simetría y una línea de reflexión

En el fascinante mundo de la geometría, nos encontramos con una variedad de conceptos que nos ayudan a comprender la simetría en las figuras. Dos de estos conceptos son los ejes de simetría y las líneas de reflexión, los cuales a primera vista pueden parecer similares, pero en realidad tienen diferencias importantes.

Eje de simetría

Comencemos por definir qué es un eje de simetría. Un eje de simetría es una línea imaginaria que divide una figura en dos partes congruentes o idénticas. Esto significa que si doblamos la figura a lo largo del eje de simetría, ambas mitades coincidirán perfectamente una sobre la otra. En otras palabras, cada punto de una mitad de la figura tiene un correspondiente exacto en la otra mitad.

Los ejes de simetría pueden ser verticales, horizontales o incluso diagonales. Por ejemplo, consideremos un cuadrado. Si trazamos una línea vertical que pasa por su centro, esta línea actuará como un eje de simetría para el cuadrado. Al doblar el cuadrado a lo largo de este eje, obtendremos dos mitades que son imágenes especulares una de la otra.

Línea de reflexión

Por otro lado, una línea de reflexión es una línea recta que permite reflejar una figura a través de ella. A diferencia de los ejes de simetría, las líneas de reflexión no necesariamente dividen la figura en dos partes congruentes. En cambio, la línea de reflexión actúa como un espejo sobre el cual se refleja la figura.

Las líneas de reflexión pueden ser verticales, horizontales o incluso oblicuas. Volviendo al ejemplo del cuadrado, si trazamos una línea vertical que no pasa por su centro, esta línea actuará como una línea de reflexión para el cuadrado. Al reflejar el cuadrado a través de esta línea, obtendremos una imagen que es una versión especular, pero no necesariamente idéntica a la figura original.

Diferencias clave

• Un eje de simetría divide una figura en dos partes idénticas, mientras que una línea de reflexión simplemente refleja la figura.
• Los ejes de simetría dan lugar a dos mitades congruentes, mientras que las líneas de reflexión pueden generar imágenes especulares distintas a la figura original.
• Los ejes de simetría pueden ser verticales, horizontales o diagonales, mientras que las líneas de reflexión también pueden ser oblicuas.
• La cantidad de ejes de simetría de una figura puede variar, mientras que una figura solo tiene una línea de reflexión principal.

Tanto los ejes de simetría como las líneas de reflexión son herramientas fundamentales para comprender la simetría en las figuras geométricas. Si bien comparten ciertas similitudes, sus diferencias clave radican en cómo dividen y reflejan una figura. Además de ampliar nuestro conocimiento en geometría, explorar estos fascinantes conceptos nos permite apreciar la belleza y la armonía presentes en el mundo de las formas.

Pueden las figuras tridimensionales tener ejes de simetría

La simetría es un tema fascinante en el campo de la geometría. Nos permite identificar patrones y regularidades en las figuras, lo que a su vez nos ayuda a comprender mejor sus propiedades y características. Pero, ¿pueden las figuras tridimensionales tener ejes de simetría?

Ejes de simetría en las figuras tridimensionales

Cuando hablamos de ejes de simetría, generalmente pensamos en figuras planas como círculos, cuadrados o triángulos. Estas figuras pueden tener ejes de simetría que dividen la figura en dos partes iguales si se reflejan a lo largo del eje.

Sin embargo, en el mundo tridimensional, la situación es un poco más compleja. A diferencia de las figuras bidimensionales, las figuras tridimensionales no pueden tener ejes de simetría en el mismo sentido que las figuras planas.

En cambio, las figuras tridimensionales pueden tener planos de simetría. Un plano de simetría divide la figura en dos partes que son imágenes especulares una de la otra. Esto significa que si colocamos un espejo a lo largo del plano de simetría, la imagen reflejada será idéntica a la figura original.

Ejemplos de figuras tridimensionales con planos de simetría

Existen numerosas figuras tridimensionales con planos de simetría. Algunos ejemplos comunes incluyen cubos, prismas, pirámides y cilindros.

Un cubo, por ejemplo, tiene múltiples planos de simetría. Si imaginamos un plano que atraviesa el cubo desde una esquina hasta la esquina opuesta, esta división creará dos mitades iguales. Además, también puede haber planos de simetría en todas las caras del cubo.

Los prismas y las pirámides también pueden tener planos de simetría. Estos planos se extienden a lo largo de las caras de estas figuras y crean divisiones simétricas.

Incluso los cilindros pueden tener planos de simetría. Imagina un plano que corta el cilindro en el medio, dividiendo la figura en dos partes simétricas.

Estos ejemplos nos muestran que aunque las figuras tridimensionales no pueden tener ejes de simetría como las figuras bidimensionales, aún existen propiedades simétricas en estas formas geométricas más complejas.

Si estás explorando el fascinante mundo de la geometría tridimensional, ten en cuenta que las figuras pueden tener planos de simetría en lugar de ejes de simetría. Estos planos de simetría te ayudarán a comprender mejor las propiedades y regularidades de estas figuras, ampliando así tu conocimiento sobre geometría.

Preguntas frecuentes (FAQ)

1. ¿Qué es un eje de simetría?

Un eje de simetría es una línea imaginaria que divide una figura en dos partes iguales y opuestas.

2. ¿Cuántos ejes de simetría puede tener una figura?

Una figura puede tener varios ejes de simetría, incluso puede no tener ningún eje de simetría.

3. ¿Cómo identificar si una figura tiene un eje de simetría?

Para identificar si una figura tiene un eje de simetría, es necesario buscar una línea en la que los elementos de la figura se reflejen de manera idéntica en ambos lados.

4. ¿Se pueden encontrar ejes de simetría en figuras tridimensionales?

No, los ejes de simetría solo se pueden encontrar en figuras bidimensionales, como cuadrados, círculos o triángulos.

5. ¿Cómo se usan los ejes de simetría en geometría?

Los ejes de simetría son utilizados para estudiar y describir propiedades de las figuras geométricas, así como también se emplean en el diseño gráfico y la arquitectura.