Distribución de Probabilidad: Descubre cómo calcular y aplicar este concepto clave en estadística

La distribución de probabilidad es un concepto clave en estadística que permite analizar y entender cómo se distribuyen los datos en un conjunto. En el campo de la estadística, existen diferentes tipos de distribuciones de probabilidad que se utilizan para modelar fenómenos aleatorios y predecir resultados.

Exploraremos en detalle qué es una distribución de probabilidad, cómo se calcula y cuáles son sus aplicaciones prácticas. Veremos ejemplos de las distribuciones más comunes, como la distribución normal, binomial, de Poisson y exponencial, entre otras. Además, aprenderás a utilizar herramientas como gráficos y tablas para representar estas distribuciones y realizar inferencias estadísticas.

Qué es la distribución de probabilidad y cómo se utiliza en estadística

La distribución de probabilidad es un concepto fundamental en estadística que nos permite describir y analizar el comportamiento de variables aleatorias. En términos simples, se trata de una función matemática que asigna una probabilidad a cada valor posible que puede tomar una variable aleatoria.

Para entender mejor este concepto, pensemos en un ejemplo. Supongamos que estamos lanzando un dado justo de seis caras. La variable aleatoria en este caso sería el resultado del lanzamiento, que puede ser cualquier número del 1 al 6. La distribución de probabilidad nos dirá la probabilidad de obtener cada uno de estos valores.

Existen diferentes tipos de distribuciones de probabilidad, siendo las más comunes la distribución uniforme, la distribución binomial, la distribución normal y la distribución de Poisson. Cada una de estas distribuciones tiene características particulares y se utiliza en diferentes contextos según las propiedades de la variable aleatoria que estamos estudiando.

Cómo calcular la distribución de probabilidad

El cálculo de la distribución de probabilidad depende del tipo de distribución que estemos considerando. Cada distribución tiene una fórmula específica para calcular la probabilidad de cada valor posible.

En el caso de la distribución uniforme, por ejemplo, todos los valores tienen la misma probabilidad. Si tenemos una variable aleatoria que puede tomar valores entre a y b, la fórmula para calcular la probabilidad de un valor x específico sería:

P( = x) = 1 / (b - a + 1)

En cambio, si estamos trabajando con una distribución binomial, que modela el número de éxitos en una serie de n ensayos independientes y tiene una tasa de éxito p constante, la fórmula para calcular la probabilidad de obtener k éxitos sería:

P( = k) = C(n, k) * p^k * (1 - p)^(n - k)

Donde C(n, k) es el coeficiente binomial, que se calcula como:

C(n, k) = n! / (k!(n - k)!)

Estas son solo algunas de las fórmulas utilizadas para calcular la distribución de probabilidad en diferentes contextos. En cada caso, es importante conocer las propiedades de la distribución y cómo aplicar correctamente la fórmula correspondiente.

Aplicaciones de la distribución de probabilidad

La distribución de probabilidad se utiliza en una amplia variedad de campos y disciplinas, ya que permite modelar y analizar fenómenos aleatorios. Algunas de las aplicaciones más comunes son:

• Economía y finanzas: La distribución normal se utiliza para modelar rendimientos financieros, precios de activos y otros fenómenos relacionados con el mercado.
• Biología: Se utiliza para modelar características hereditarias, tasas de mutación y otros aspectos genéticos.
• Ingeniería: Permite modelar el tiempo de vida útil de componentes y sistemas, así como el rendimiento de procesos industriales.
• Medicina: Se utiliza para analizar la eficacia de tratamientos, el riesgo de enfermedades y otros aspectos relacionados con salud.

Estas son solo algunas de las muchas aplicaciones de la distribución de probabilidad en distintas áreas. En general, su uso ayuda a tener una mejor comprensión de fenómenos aleatorios y tomar decisiones basadas en datos probabilísticos.

Cuáles son los diferentes tipos de distribuciones de probabilidad más comunes

En estadística, la distribución de probabilidad es una herramienta fundamental para comprender y analizar el comportamiento de los datos. Existen diferentes tipos de distribuciones de probabilidad que se utilizan según el tipo de variable aleatoria con la que estemos trabajando. En este artículo, exploraremos algunos de los tipos de distribuciones de probabilidad más comunes y cómo calcularlos.

Distribución Uniforme

La distribución uniforme es uno de los tipos más simples de distribución de probabilidad. En esta distribución, todas las variables tienen la misma probabilidad de ocurrir, es decir, la probabilidad de cada valor posible es constante. Por ejemplo, en un dado justo de seis caras, cada número del 1 al 6 tiene la misma probabilidad de salir.

Distribución Normal

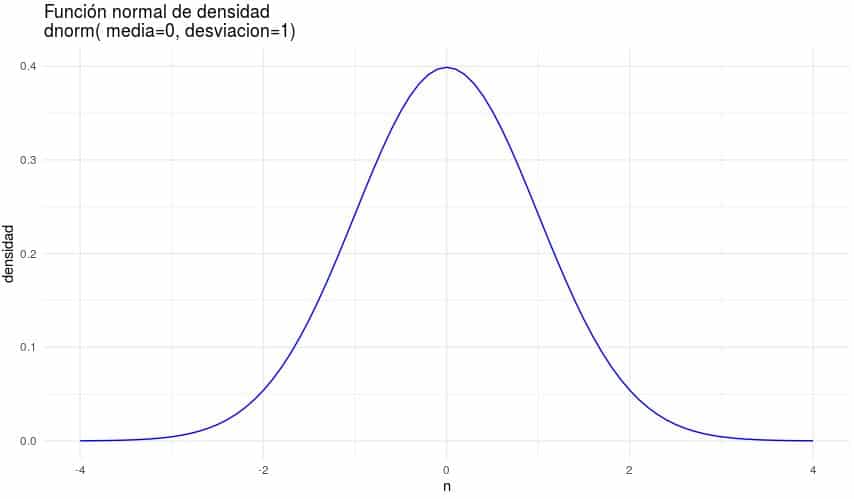
La distribución normal, también conocida como distribución de Gauss o campana de Gauss, es uno de los tipos más importantes y ampliamente utilizados en estadística. Esta distribución es simétrica y se caracteriza por tener una forma de campana. En una distribución normal, la media, la mediana y la moda son iguales, y aproximadamente el 68% de los datos se encuentran dentro de un desviación estándar de la media.

Distribución Binomial

La distribución binomial se utiliza cuando estamos trabajando con experimentos que solo tienen dos resultados posibles: éxito o fracaso. Cada prueba se considera independiente de las demás y tiene una probabilidad constante de éxito. Por ejemplo, analizar el número de veces que una moneda cae cara en un número específico de lanzamientos sería un ejemplo de distribución binomial.

Distribución de Poisson

La distribución de Poisson se utiliza cuando estamos interesados en el número de eventos que ocurren en un intervalo de tiempo específico o en un área determinada. Esta distribución es útil para modelar eventos raros o poco frecuentes, donde la probabilidad de que ocurran varios eventos en un intervalo de tiempo o área determinada es muy pequeña. Por ejemplo, analizar el número de llamadas telefónicas recibidas en un centro de atención durante un período de tiempo específico sería un ejemplo de distribución de Poisson.

Distribución Exponencial

La distribución exponencial se utiliza para modelar el tiempo entre eventos sucesivos en un proceso de Poisson. Esta distribución es útil cuando estamos interesados en el tiempo que tarda en ocurrir un evento después de que haya ocurrido otro. Por ejemplo, analizar el tiempo entre llegadas de clientes a un restaurante sería un ejemplo de distribución exponencial.

• Otro tipo de distribución de probabilidad es la distribución de Bernoulli, que se utiliza cuando solo hay dos resultados posibles: éxito o fracaso, pero a diferencia de la distribución binomial, solo se realiza una única prueba.
• Estas son solo algunas de las distribuciones de probabilidad más comunes utilizadas en estadística. Cada una tiene características y propiedades únicas que las hacen adecuadas para diferentes situaciones y tipos de datos. Es importante comprender cómo calcular y aplicar estos conceptos clave, ya que pueden proporcionar información valiosa para la toma de decisiones y el análisis de datos en diversos campos.

Cómo se calcula la media, la mediana y la moda de una distribución de probabilidad

La distribución de probabilidad es un concepto fundamental en estadística que nos permite comprender la variabilidad y la incertidumbre en diferentes fenómenos. Al analizar una distribución de probabilidad, hay tres medidas centrales clave que nos ayudan a resumir la información: la media, la mediana y la moda.

Cálculo de la media

La media es el promedio de todos los valores en una distribución de probabilidad. Para calcularlo, sumamos todos los valores y luego dividimos la suma por el número total de elementos en la distribución. Esta medida es particularmente útil cuando queremos obtener una descripción general de los datos y cuando los valores no están demasiado sesgados.

Ejemplo:

• Supongamos que tenemos la siguiente distribución de probabilidad: 2, 4, 6, 6, 8
• Sumamos todos los valores: 2 + 4 + 6 + 6 + 8 = 26
• Dividimos la suma por el número total de elementos: 26 / 5 = 5.2

Por lo tanto, la media de esta distribución de probabilidad es 5.2.

Cálculo de la mediana

La mediana es el valor central en una distribución de probabilidad cuando los datos se ordenan de menor a mayor. Para calcularla, debemos seguir los siguientes pasos:

1. Ordenar los valores de menor a mayor.
2. Si el número total de elementos es impar, la mediana es el valor que se encuentra en la posición central. Si el número total de elementos es par, la mediana es el promedio de los dos valores centrales.

Ejemplo:

• Supongamos que tenemos la siguiente distribución de probabilidad: 4, 6, 2, 8, 6
• Ordenamos los valores de menor a mayor: 2, 4, 6, 6, 8
• Como el número total de elementos es impar (5 elementos), la mediana es el valor que se encuentra en la posición central. En este caso, la mediana es 6.

Cálculo de la moda

La moda es el valor que ocurre con mayor frecuencia en una distribución de probabilidad. Para calcularla, debemos identificar cuál o cuáles son los valores con mayor frecuencia.

Ejemplo:

• Supongamos que tenemos la siguiente distribución de probabilidad: 2, 4, 6, 6, 8
• En esta distribución, el valor 6 ocurre con mayor frecuencia (2 veces), mientras que los demás valores solo ocurren una vez.

Por lo tanto, la moda de esta distribución de probabilidad es 6.

La media, la mediana y la moda son medidas importantes para entender una distribución de probabilidad. Cada una proporciona información única sobre la tendencia central de los datos y nos ayuda a resumir la información de manera concisa y significativa. Al utilizar estas medidas en combinación, podemos obtener una visión más completa y precisa de nuestra distribución de probabilidad.

Cuál es la importancia de la desviación estándar en una distribución de probabilidad

La desviación estándar es una medida estadística que juega un papel crucial en las distribuciones de probabilidad. Esta medida nos indica cuánto se alejan los valores de una distribución de su promedio o media.

En una distribución de probabilidad, la desviación estándar nos proporciona información sobre qué tan dispersos están los datos alrededor del valor medio. Una desviación estándar alta indica que los datos están más dispersos y son menos predecibles, mientras que una desviación estándar baja significa que los datos están más agrupados y son más predecibles.

Cómo calcular la desviación estándar

El cálculo de la desviación estándar implica varios pasos:

1. Calcular la media de los valores de la distribución.
2. Restar cada valor de la media y elevarlo al cuadrado.
3. Sumar todos los resultados obtenidos en el paso anterior.
4. Dividir la suma de los resultados entre el número total de valores.
5. Finalmente, tomar la raíz cuadrada del resultado obtenido en el paso anterior.

Este proceso nos permite obtener la desviación estándar de una distribución de probabilidad y nos ayuda a comprender cómo se distribuyen los datos alrededor de la media.

Aplicaciones de la desviación estándar en la interpretación de los datos

La desviación estándar tiene varias aplicaciones importantes en la interpretación de los datos:

• Identificar valores atípicos: La desviación estándar nos permite identificar valores que se alejan significativamente de la media. Estos valores podrían indicar eventos inusuales o errores en la recolección de datos.
• Comparar distribuciones: Al comparar diferentes distribuciones de probabilidad, la desviación estándar puede ayudarnos a determinar cuál es más dispersa o menos dispersa.
• Evaluar la precisión de una estimación: Si utilizamos la desviación estándar para calcular intervalos de confianza, podemos evaluar la precisión de nuestras estimaciones y medir qué tan cerca estamos del valor real.

La desviación estándar es una herramienta fundamental en el análisis estadístico, ya que nos permite comprender la distribución de los datos y su variabilidad. Su cálculo y aplicación adecuados nos proporcionan información clave para tomar decisiones informadas basadas en datos.

Cómo se interpreta la forma de una distribución de probabilidad

La forma de una distribución de probabilidad nos brinda información importante sobre cómo se distribuyen los valores en un conjunto de datos. Al interpretar la forma de una distribución, podemos entender mejor las características y el comportamiento de los datos.

Existen diferentes formas de distribuciones de probabilidad, cada una con sus propias características distintivas. Algunas de las formas más comunes son:

• La distribución normal: Esta es una de las distribuciones más conocidas y utilizadas en estadística. Tiene una forma de campana simétrica alrededor de su media y desviación estándar.
• La distribución uniforme: En esta distribución, todos los valores tienen la misma probabilidad de ocurrir. La forma de esta distribución es una línea recta constante.
• La distribución exponencial: Esta distribución se utiliza comúnmente para modelar tiempos de espera o procesos de decaimiento. Su forma es asimétrica y presenta una cola larga hacia la derecha.
• La distribución de Poisson: Se utiliza para modelar eventos raros o discretos que ocurren en un intervalo de tiempo o espacio fijo. Su forma es asimétrica y puede parecerse a la distribución exponencial en ciertos casos.

Al observar la forma de una distribución de probabilidad, podemos analizar si los datos están sesgados, simétricos, concentrados en ciertos rangos o dispersos. Esto puede ser útil para entender mejor los patrones en los datos y tomar decisiones informadas.

Es importante destacar que la forma de una distribución puede variar dependiendo del conjunto de datos que estemos analizando. Por lo tanto, es fundamental realizar un análisis cuidadoso y utilizar las herramientas estadísticas adecuadas para identificar la forma de la distribución.

Interpretar la forma de una distribución de probabilidad nos permite comprender cómo se distribuyen los valores en un conjunto de datos. Existen diferentes formas de distribuciones de probabilidad, cada una con características distintivas. Al analizar la forma de la distribución, podemos obtener información valiosa sobre los datos y tomar decisiones informadas basadas en dicho análisis.

Qué es el teorema del límite central y cómo se aplica en la distribución de probabilidad

El teorema del límite central es uno de los conceptos fundamentales en estadística y está estrechamente relacionado con la distribución de probabilidad. Para entenderlo, primero necesitamos comprender qué es la distribución de probabilidad.

En estadística, la distribución de probabilidad nos permite describir cómo se distribuyen los posibles valores de una variable aleatoria. Una variable aleatoria puede ser cualquier cantidad que pueda tomar diferentes valores, como el lanzamiento de un dado, el tiempo que tarda en llegar un autobús o incluso el rendimiento de una acción en el mercado. La función de distribución de probabilidad asigna probabilidades a cada posible valor que puede tomar la variable.

Existen diferentes tipos de distribuciones de probabilidad, como la distribución normal, la distribución uniforme, la distribución binomial y muchas otras. Cada distribución tiene sus propias características y se utiliza en diferentes situaciones.

Una vez que comprendemos la distribución de probabilidad, podemos adentrarnos en el teorema del límite central. Este teorema establece que, bajo ciertas condiciones, la suma o media de un gran número de variables aleatorias independientes e idénticamente distribuidas seguirá una distribución aproximadamente normal, independientemente de la forma de la distribución original.

En otras palabras, si tomamos una muestra aleatoria de tamaño n de una población, calculamos la media de esa muestra y repetimos este proceso muchas veces, las medias resultantes seguirán una distribución normal. Esto es particularmente útil cuando la distribución original no es normal y queremos trabajar con la media de la población.

El teorema del límite central tiene una amplia variedad de aplicaciones en estadística. Por ejemplo, es utilizado para estimar intervalos de confianza, realizar pruebas de hipótesis y realizar predicciones basadas en muestras de datos. También proporciona una base teórica para otros conceptos clave, como la regresión lineal y el análisis de varianza.

El teorema del límite central es un importante concepto en estadística que nos permite trabajar con la distribución de probabilidad de variables aleatorias. Nos permite hacer inferencias sobre poblaciones utilizando muestras de datos y nos da la base para muchas técnicas estadísticas.

Cómo se usa la distribución normal estándar en estadística

La distribución normal estándar, también conocida como la distribución de Gauss o la campana de Gauss, es una de las distribuciones de probabilidad más importantes en estadística. Se utiliza ampliamente para modelar fenómenos naturales y sociales que tienden a agruparse alrededor de un valor central.

Para utilizar la distribución normal estándar en estadística, primero es necesario entender sus características principales. Esta distribución es simétrica alrededor de su media, que es igual a cero, y tiene una desviación estándar de uno. Su forma característica es la de una curva en forma de campana, lo que implica que la mayoría de los datos se encuentran cerca de la media y la probabilidad de valores extremos disminuye a medida que nos alejamos de ella.

Cómo calcular la distribución normal estándar

Calcular los valores específicos de la distribución normal estándar implica el uso de una tabla de valores z estándar, que muestra las áreas bajo la curva de la distribución normal estándar correspondientes a diferentes intervalos de z-score. El z-score es una medida estandarizada utilizada para describir la posición de un valor con respecto a la media.

Una vez que tenemos el z-score de interés, podemos consultar la tabla de valores z para encontrar el área correspondiente bajo la curva de la distribución normal estándar. Este área representa la probabilidad acumulativa hasta ese punto específico.

Además del cálculo utilizando la tabla de valores z, también es posible utilizar software estadístico como R o Python para obtener los valores de la distribución normal estándar de manera más rápida y precisa.

Aplicaciones de la distribución normal estándar

La distribución normal estándar tiene diversas aplicaciones en estadística. Una de las principales es el cálculo de probabilidades para eventos que se distribuyen normalmente.

Por ejemplo, supongamos que queremos determinar la probabilidad de que una persona seleccionada al azar tenga una altura entre ciertos valores. Al conocer la media y la desviación estándar de la distribución de alturas de la población, podemos utilizar la distribución normal estándar para calcular la probabilidad de que un valor aleatorio se encuentre dentro de ese rango específico.

Otra aplicación común es la realización de pruebas de hipótesis en estadística. Al asumir que los datos siguen una distribución normal, podemos utilizar la distribución normal estándar para calcular valores críticos y tomar decisiones sobre aceptar o rechazar una hipótesis nula.

La distribución normal estándar es una herramienta fundamental en estadística para modelar fenómenos naturales y sociales. Su utilización requiere del cálculo de áreas bajo su curva mediante tablas de valores z o software estadístico adecuado. Además, tiene múltiples aplicaciones prácticas, desde el cálculo de probabilidades hasta la realización de pruebas de hipótesis.

Cuáles son las principales características de la distribución binomial y cómo se aplica en problemas prácticos

La distribución binomial es un tipo de distribución de probabilidad discreta que se utiliza para modelar el resultado de un experimento o proceso en el cual se pueden tener dos resultados posibles: éxito o fracaso, sí o no, 1 o 0. Esta distribución es muy común en problemas donde se realizan una serie de ensayos independientes entre sí y se desea conocer la probabilidad de obtener un número específico de éxitos.

Las características principales de la distribución binomial son las siguientes:

• Cada ensayo debe ser independiente del otro, es decir, el resultado de un ensayo no afecta el resultado de los otros ensayos.
• El ensayo debe tener solo dos posibles resultados: éxito o fracaso.
• La probabilidad de éxito debe permanecer constante en todos los ensayos.
• El número total de ensayos debe ser fijo y conocido de antemano.

Para calcular la probabilidad de obtener un número específico de éxitos en una distribución binomial, se utiliza la fórmula de la probabilidad binomial:

P( = k) = C(n, k) * p^k * (1-p)^(n-k)

Donde:

• P( = k) es la probabilidad de obtener exactamente k éxitos.
• C(n, k) representa el coeficiente binomial, que se calcula como n! / (k! * (n-k)!), siendo n el número total de ensayos y k el número de éxitos que se desea obtener.
• p es la probabilidad de éxito en un solo ensayo.
• (1-p) es la probabilidad de fracaso en un solo ensayo.
• n es el número total de ensayos.

La distribución binomial tiene numerosas aplicaciones en problemas prácticos, como en estudios de fiabilidad, análisis de riesgo, investigación médica, control de calidad, entre otros. Por ejemplo, supongamos que queremos conocer la probabilidad de que exactamente 3 de 5 estudiantes aprueben un examen con una tasa de éxito del 60%. Utilizando la fórmula de la probabilidad binomial, podemos calcular:

P( = 3) = C(5, 3) * 0.6^3 * (1-0.6)^(5-3) = 10 * 0.216 * 0.16 = 0.3456

Por lo tanto, la probabilidad de que exactamente 3 estudiantes aprueben el examen es del 34.56%.

La distribución binomial es una herramienta fundamental para el cálculo de probabilidades en problemas donde se tienen ensayos independientes con dos resultados posibles. Su aplicación es amplia y puede ayudarnos a tomar decisiones basadas en la probabilidad de obtener un número específico de éxitos.

Qué es la distribución de Poisson y en qué situaciones se utiliza

La distribución de Poisson es un modelo matemático utilizado para calcular la probabilidad de ocurrencia de un evento en un intervalo específico de tiempo o espacio. Es aplicado en situaciones en las que se busca analizar y predecir eventos que ocurren de forma aleatoria e independiente, pero con una tasa media conocida.

Una distribución de Poisson se caracteriza por tener las siguientes propiedades:

1. La probabilidad de cualquier número de eventos en un intervalo dado es proporcional a la longitud de dicho intervalo.
2. La probabilidad de que ocurra más de un evento en un intervalo infinitesimalmente pequeño tiende a ser cero.
3. La probabilidad de que ocurra exactamente un evento se mantiene constante independientemente del tamaño del intervalo.
4. La ocurrencia de eventos es independiente entre intervalos de tiempo o espacio.

La distribución de Poisson se utiliza en una amplia gama de aplicaciones en diferentes campos, tales como:

• Estadística: para modelar el número de eventos que ocurren en un período de tiempo determinado, como la cantidad de llamadas telefónicas recibidas en un centro de atención al cliente en una hora.
• Biología: para estudiar la distribución de especies en un área geográfica determinada.
• Física: para analizar el tiempo transcurrido entre eventos radiactivos en experimentos nucleares.
• Tiempo: para pronosticar la tasa de llegada de clientes a un comercio en determinadas horas del día.

La distribución de Poisson es un concepto clave en estadística que permite modelar y predecir eventos aleatorios en intervalos de tiempo o espacio. Su aplicación abarca diferentes campos y su cálculo se basa en la tasa media de ocurrencia de los eventos.

Cómo se calculan las probabilidades utilizando la distribución de probabilidad en un caso práctico

La distribución de probabilidad es un concepto clave en estadística que nos permite calcular las probabilidades asociadas a diferentes eventos. Al comprender cómo calcular y aplicar esta distribución, podemos realizar análisis más detallados y tomar decisiones informadas en diversos contextos.

¿Qué es la distribución de probabilidad?

La distribución de probabilidad es una función matemática que describe la probabilidad de ocurrencia de cada resultado posible para una variable aleatoria en particular. En otras palabras, nos permite conocer las posibilidades de obtener distintos valores de una variable en un experimento o fenómeno aleatorio.

Existen diferentes tipos de distribuciones de probabilidad, como la distribución normal, la distribución binomial y la distribución uniforme, entre otras. Cada una de estas distribuciones se utiliza en situaciones específicas y nos ayuda a comprender mejor los datos y eventos observados.

Cómo calcular las probabilidades utilizando la distribución de probabilidad

El cálculo de las probabilidades utilizando la distribución de probabilidad depende del tipo de distribución que estemos utilizando. A continuación, vamos a ver un caso práctico utilizando la distribución normal, una de las distribuciones más comunes.

Supongamos que estamos estudiando el rendimiento de estudiantes en un examen y sabemos que la media de calificaciones es de 75 y la desviación estándar es de 10. Queremos saber cuál es la probabilidad de que un estudiante obtenga una calificación superior a 85.

Para realizar este cálculo, necesitamos utilizar la fórmula de la distribución normal estándar, que consiste en restar la media y dividir por la desviación estándar:

Z = ( - μ) / σ

En este caso, representa la calificación que queremos analizar, μ es la media y σ es la desviación estándar. En nuestro ejemplo, sería igual a 85, μ es igual a 75 y σ es igual a 10.

Una vez que obtengamos el valor de Z, lo consultamos en una tabla de valores Z para obtener la probabilidad correspondiente. Para nuestro caso, debemos buscar la probabilidad asociada a Z = (85 - 75) / 10 = 1.

Si consultamos la tabla de valores Z, encontraremos que la probabilidad de obtener un Z de 1 es aproximadamente 0.8413.

Finalmente, podemos concluir que la probabilidad de que un estudiante obtenga una calificación superior a 85 es del 84.13%.

Aplicaciones de la distribución de probabilidad

La distribución de probabilidad tiene numerosas aplicaciones en diferentes áreas, desde la economía hasta la medicina y la ingeniería. Algunos ejemplos de cómo se aplica esta distribución incluyen:

• Modelización de fenómenos naturales, como el tiempo atmosférico o la temperatura.
• Análisis de riesgo financiero y estimación de pérdidas o ganancias potenciales.
• Evaluación de la eficacia de tratamientos médicos en ensayos clínicos.
• Optimización de procesos y planificación de la producción en ingeniería.

Estas son solo algunas de las muchas formas en que la distribución de probabilidad se aplica en diversas disciplinas. Su capacidad para describir e interpretar datos aleatorios es fundamental para comprender fenómenos complejos y tomar decisiones fundamentadas basadas en la incertidumbre inherente a estos eventos.

La distribución de probabilidad es un concepto clave en estadística que nos permite calcular y aplicar probabilidades en diferentes contextos. A través del cálculo utilizando fórmulas específicas para cada tipo de distribución, podemos obtener información valiosa sobre los eventos y tomar decisiones informadas basadas en la incertidumbre asociada a los datos aleatorios.

Preguntas frecuentes (FAQ)

1. ¿Qué es una distribución de probabilidad?

Una distribución de probabilidad es una función matemática que describe la probabilidad de ocurrencia de cada posible resultado en un experimento aleatorio.

2. ¿Cuáles son los tipos más comunes de distribuciones de probabilidad?

Los tipos más comunes de distribuciones de probabilidad son la distribución normal, la distribución binomial, la distribución de Poisson y la distribución uniforme.

3. ¿Cómo se calcula la media de una distribución de probabilidad?

La media de una distribución de probabilidad se calcula multiplicando cada valor por su respectiva probabilidad y luego sumando todos los resultados.

4. ¿Qué es el percentil en una distribución de probabilidad?

El percentil en una distribución de probabilidad indica el valor por debajo del cual se encuentra cierto porcentaje de los datos.

5. ¿Cuál es la importancia de la distribución de probabilidad en estadística?

La distribución de probabilidad es importante en estadística porque permite modelar y entender el comportamiento de variables aleatorias, hacer predicciones y tomar decisiones basadas en la probabilidad.