Nombres de los números después del punto decimal: Aprende cómo llamarlos y domina su significado
Los números después del punto decimal, también conocidos como decimales, son una parte fundamental de las matemáticas. Estos números nos permiten representar fracciones y cantidades más precisas que no pueden ser expresadas utilizando solo números enteros. Conocer cómo nombrar y entender el significado de los dígitos en la parte decimal es esencial para muchas áreas de estudio, como la física, la economía y la estadística.
Exploraremos los nombres de los números después del punto decimal y cómo se relacionan con su valor. Aprenderemos sobre los distintos términos utilizados, como décimas, centésimas, milésimas, etc. También veremos ejemplos prácticos que ilustran cómo utilizar estos términos en problemas numéricos. Al finalizar la lectura, tendrás una sólida comprensión de cómo llamar a los números después del punto decimal y podrás aplicarlo en diferentes situaciones matemáticas.
- Cómo se llaman los números después del punto decimal
- Cuál es el significado de los números decimales
- Cuántos números decimales existen
- Qué es un número decimal periódico
- Cómo se representa un número decimal periódico
- Qué es un número decimal no periódico
- Puedes dar ejemplos de números decimales no periódicos
- Cuál es la diferencia entre una fracción decimal y un número decimal
- Cuáles son los nombres de los primeros números decimales
- Preguntas frecuentes (FAQ)
Cómo se llaman los números después del punto decimal
Los números después del punto decimal son conocidos como números decimales. Estos números son fundamentales en las matemáticas y se utilizan para representar fracciones y valores más precisos que los números enteros.
Cuando nos referimos a los números decimales, es importante conocer cómo llamarlos correctamente según la posición que ocupen en relación al punto decimal. Esto nos permitirá comunicarnos con mayor claridad y precisión en diferentes contextos.
Números enteros
Antes de adentrarnos en los nombres específicos de los números decimales, es importante recordar cómo nombrar a los números enteros. Los números enteros son aquellos que no tienen parte decimal, es decir, no tienen números después del punto decimal. Por ejemplo, 5, -12 y 0 son números enteros.
Números decimales básicos
Cuando un número decimal tiene una parte entera seguida de una única cifra decimal, esta se llama décima. Por ejemplo, el número 3.6 tiene una parte entera de 3 y una décima de 6. Del mismo modo, si tenemos el número -1.2, la parte entera es -1 y la décima es 2.
Si un número decimal tiene dos cifras decimales, la primera se llama centésima y la segunda se llama milésima. Por ejemplo, si tenemos el número 0.45, la parte entera es 0, la décima es 4, la centésima es 5 y no hay milésimas. Si el número es -0.78, la parte entera es 0, la décima es 7, la centésima es 8 y no hay milésimas.
Números decimales con más de dos cifras
Cuando un número decimal tiene más de dos cifras decimales, se sigue una nomenclatura similar pero utilizando prefijos que representan potencias de diez. Estos prefijos le dan nombre a cada uno de los dígitos decimales que siguen después del punto decimal.
Si un número tiene tres cifras decimales, la primera que representa las décimas se llama milésima, la segunda que representa las centésimas se llama diezmilésima y la tercera que representa las milésimas se llama cienmilésima.
Para ejemplificar esto, consideremos el número 1.234. La parte entera es 1, las décimas son 2, las centésimas son 3 y las milésimas son 4. Así, su descomposición quedaría como: 1 + 2/10 + 3/100 + 4/1000.
En general, si un número decimal tiene n cifras decimales, la i-ésima posición desde la derecha hacia la izquierda se llama diez elevado a la -i potencia (por ejemplo, décima para i=1, centésima para i=2, etc.)
Uso y aplicaciones de los nombres de los números decimales
Conocer los nombres y la notación para los números decimales es de vital importancia en diferentes áreas, como la matemática, la física, la economía y las ciencias en general.
En matemáticas, los números decimales permiten realizar cálculos más precisos y representar de manera exacta cantidades que no pueden expresarse como fracciones. Además, son fundamentales para el estudio de conceptos como la proporcionalidad y las operaciones aritméticas básicas.
En física, los números decimales son utilizados para medir magnitudes, como distancias, masas y tiempos, con gran precisión. De esta forma, se pueden realizar cálculos y experimentos que requieren resultados más detallados.
En economía y finanzas, los números decimales son utilizados para representar valores monetarios y tasas de interés. Esto permite realizar cálculos y análisis financieros más precisos y tomar decisiones fundamentadas en inversiones y préstamos.
Finalmente, en las ciencias en general, los números decimales se utilizan para representar cantidades que no son enteras ni fraccionarias, como densidades, velocidades o concentraciones. Estos valores son esenciales para el desarrollo e investigación científica en diversas disciplinas.
Conocer cómo se llaman y comprenden los números después del punto decimal nos proporciona una herramienta fundamental para comunicarnos y trabajar con mayor precisión en diferentes áreas del conocimiento. Su dominio nos permite expresar tanto valores simples como cantidades extremadamente precisas, facilitando así el entendimiento y análisis de nuestros datos y resultados.
Cuál es el significado de los números decimales
Los números decimales son aquellos que se encuentran después del punto decimal en una forma numérica. Estos números representan una parte o fracción de un número entero y nos permiten expresar valores más precisos que los números enteros.
En el sistema decimal, cada posición después del punto representa una potencia negativa de 10. Por ejemplo, el número 0.1 significa "un décimo" o "una décima parte" de un entero. Los números decimales también pueden representar fracciones mayores que uno, como 1.5, que significa "un entero y medio" o "una fracción igual a tres medios".
Entender el significado de los números decimales es fundamental para poder interpretar y utilizar adecuadamente las medidas, las cantidades y los cálculos matemáticos que involucran estas fracciones numéricas.
Nombres de los números decimales según su posición
Cuando nos referimos a los números decimales, podemos utilizar diferentes términos para describir su valor según la posición que ocupan. A continuación, te presento algunos términos comunes:
- Décimas: Los números decimales que tienen una posición inmediatamente detrás del punto decimal se llaman décimas. Por ejemplo, en el número 0.7, el 7 es una décima.
- Centésimas: Los números decimales que ocupan la segunda posición después del punto decimal se denominan centésimas. Por ejemplo, en el número 0.25, el 2 es una centésima.
- Milésimas: Los números decimales que se encuentran en la tercera posición después del el punto decimal reciben el nombre de milésimas. Por ejemplo, en el número 0.003, el 3 es una milésima.
Estos son solo algunos ejemplos, pero los números decimales pueden tener posiciones aún más allá del punto decimal, como diezmilésimas, cienmilésimas y así sucesivamente.
Lectura y escritura de números decimales
Cuando leemos o escribimos números decimales, es importante simbolizar adecuadamente las fracciones numéricas para evitar confusiones. Para ello, se utilizan palabras o símbolos específicos para cada posición después del punto decimal:
- Escribir números decimales: La forma común de escribir números decimales en español es colocar una coma (,) como separador entre la parte entera y la parte decimal. Por ejemplo, en lugar de 1.5, se escribiría como 1,5.
- Lectura de números decimales: Al leer números decimales, generalmente se dice "coma" antes de mencionar la parte decimal. Por ejemplo, el número 0.7 se leería como "cero coma siete".
Es fundamental comprender y aplicar correctamente estas convenciones al leer y escribir números decimales para garantizar una comunicación clara y precisa en contextos matemáticos y científicos.
Cuántos números decimales existen
Los números decimales son una parte fundamental de las matemáticas y se utilizan en diversas situaciones en nuestra vida cotidiana. Estos números se componen de dos partes principales: la parte entera y la parte decimal. La parte entera representa los números naturales y la parte decimal representa valores fraccionarios o aquellos que están después del punto decimal.
Es importante destacar que los números decimales pueden tener infinitas cifras decimales, lo que significa que hay una gran cantidad de números después del punto decimal. Sin embargo, dentro de esta infinidad de cifras, existen algunos nombres particulares para ciertos grupos de números decimales. A continuación, te mostraremos cuáles son estos nombres y cómo se les llama.
Números decimales comunes
Dentro de los números decimales más comunes, encontramos aquellos que tienen nombres especiales asociados a ellos. Por ejemplo, el número 0.5 se llama medio, ya que es la mitad del número 1. Del mismo modo, el número 0.25 se llama cuarto, ya que es una cuarta parte del número 1.
Otro número decimal comúnmente utilizado es el 0.75, al cual se le llama tres cuartos, ya que representa tres partes de cuatro. Además, el número 0.33 se llama un tercio, puesto que es una tercera parte de 1.
Estos nombres son ampliamente utilizados en diversos campos como la cocina, la música y el deporte, donde se requiere de medidas precisas y fracciones específicas. Conocer estos nombres nos permite comunicarnos de manera eficiente y precisa cuando hablamos de valores decimales.
Números decimales repetitivos
Existen también números decimales que se repiten y suelen tener un patrón determinado. Un ejemplo de esto es el número 0.33333..., que se pronuncia como "tres periódico" y representa un tercio infinito. Del mismo modo, el número 0.66666... se llama "seis periódico" y representa dos tercios infinitos.
Estos números decimales repetitivos son interesantes, ya que nos muestran la naturaleza infinita e irracional de ciertos valores decimales. Aunque su escritura puede resultar tediosa debido a la repetición, su significado es claro y matemáticamente preciso.
Números decimales irracionales
Finalmente, existen algunos números decimales que no se repiten y no pueden ser expresados como una fracción exacta. Estos números se conocen como irracionales y representan valores inexactos en forma decimal.
Un ejemplo clásico de un número decimal irracional es pi (π), que es aproximadamente igual a 3.14159... Su escritura decimal nunca termina ni se repite, lo que lo convierte en un número fascinante desde el punto de vista matemático.
Otro número decimal irracional ampliamente conocido es la raíz cuadrada de 2, cuyo valor decimal es aproximadamente igual a 1.41421...
Los números decimales tienen una gran variedad de nombres y significados dependiendo de las cifras que los componen. Desde números decimales comunes hasta valores repetitivos e irracionales, estos números nos permiten expresar medidas precisas y realizar cálculos matemáticos con mayor exactitud. Aprender y dominar los nombres de los números después del punto decimal es fundamental para cualquier persona interesada en las matemáticas y su aplicación en la vida cotidiana.
Qué es un número decimal periódico
Un número decimal periódico es aquel que tiene una secuencia de uno o varios dígitos que se repiten infinitamente después del punto decimal. Estos dígitos repetidos forman un patrón que se mantiene constante a lo largo del número.
En matemáticas, los números decimales periódicos se pueden representar utilizando una barra sobre los dígitos repetidos, indicando así que la secuencia se repite infinitamente. Por ejemplo, el número 0.333... representa una serie infinita de 3's.
Es importante tener en cuenta que no todos los números decimales son periódicos. Algunos números, como por ejemplo el número Pi (π), tienen una expansión decimal infinita pero no presentan una repetición periódica de dígitos. A estos números se les llama "decimales no periódicos" o "decimales no repetitivos".
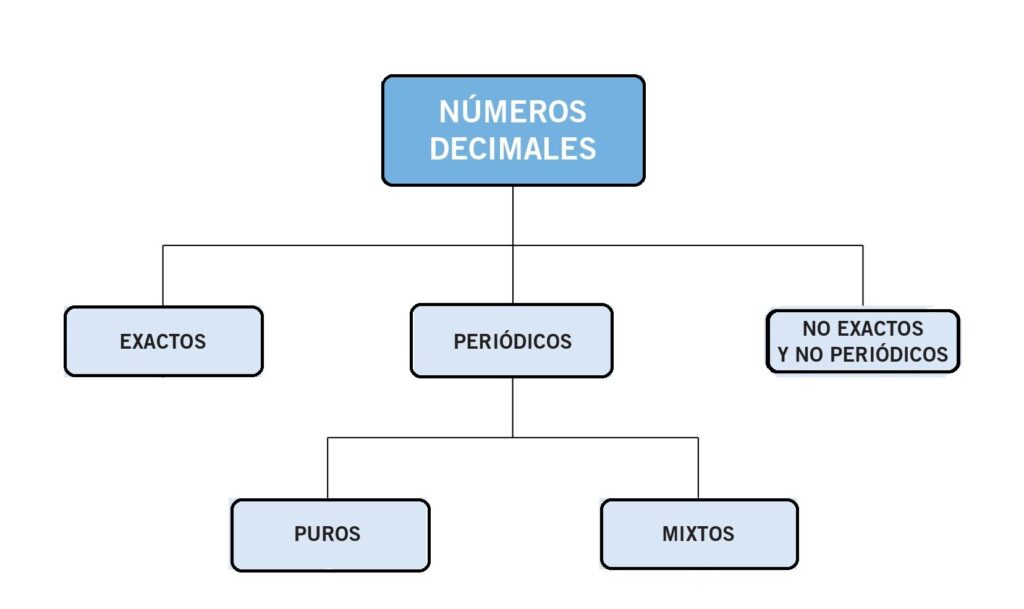
Números decimales periódicos puros y mixtos
Dentro de los números decimales periódicos, existen dos categorías: los periódicos puros y los periódicos mixtos.
Un número decimal periódico puro es aquel en el cual la secuencia de dígitos repetidos comienza justo después del punto decimal. Por ejemplo, el número 0.6666... es un número decimal periódico puro, ya que la secuencia de 6's se repite infinitamente desde el punto decimal hacia adelante.
Por otro lado, un número decimal periódico mixto es aquel en el cual la secuencia de dígitos repetidos no comienza inmediatamente después del punto decimal, sino que está separada por una parte no repetitiva. Por ejemplo, el número 1.23434343... es un número decimal periódico mixto, dado que la secuencia de 34's se repite infinitamente, pero después de una parte no repetitiva representada por los dígitos 1 y 2.
Fracciones y números decimales periódicos
Existe una relación interesante entre las fracciones y los números decimales periódicos. Muchas veces, las fracciones pueden expresarse como números decimales periódicos y viceversa.
Por ejemplo, la fracción 1/3 se puede representar de manera exacta como el número decimal periódico 0.333..., donde la secuencia de 3's se repite infintamente. De manera similar, el número decimal periódico puro 0.666... puede ser expresado como la fracción 2/3.
Cuando una fracción se puede convertir en un número decimal periódico, se dice que es una fracción periódica. Este tipo de fracciones se pueden escribir utilizando una línea horizontal encima de los dígitos que se repiten, similar a la representación de los números decimales periódicos. Por ejemplo, la fracción 5/9 se puede expresar como el número decimal periódico 0.555...
Los números decimales periódicos son aquellos que presentan una secuencia de dígitos repetidos infinitamente después del punto decimal. Pueden ser clasificados como periódicos puros o periódicos mixtos, dependiendo de si la secuencia repetida comienza inmediatamente después del punto decimal o si hay una parte no repetitiva antes. Los números decimales periódicos pueden representar tanto fracciones como cantidades exactas, y viceversa.
Cómo se representa un número decimal periódico
Los números decimales periódicos son aquellos que tienen una secuencia de dígitos que se repite infinitamente. Para representar correctamente un número decimal periódico en notación decimal, es necesario utilizar algunos símbolos y técnicas específicas.
En primer lugar, se debe identificar la secuencia de dígitos que se repite. Esta secuencia se encierra entre paréntesis para indicar su repetición. Por ejemplo, si tenemos el número 0.333..., la secuencia "333" se repite infinitamente, por lo que lo escribimos como 0.(3).
Si la secuencia repetitiva se encuentra inmediatamente después del punto decimal, se puede utilizar también una línea horizontal sobre el o los dígitos repetidos para indicar su repetición. Por ejemplo, si tenemos el número 0.1616..., podemos escribirlo como 0.16̅.
Es importante destacar que cuando se trata de números decimales periódicos mixtos, es decir, aquellos que presentan una parte entera y una parte decimal repetitiva, se utilizan ambos métodos de representación mencionados anteriormente. Por ejemplo, si tenemos el número 5.272727..., la parte decimal repetitiva "2727" se encierra entre paréntesis después de una barra vertical. Por lo tanto, se representa como 5+(2)(7)̅|.
Significado de los nombres de los números decimales periódicos
Cada número decimal periódico tiene un nombre especial basado en la cantidad de dígitos que se repiten en la secuencia. Este nombre se deriva del latín y esencialmente describe la longitud de la secuencia periódica.
En primer lugar, tenemos los números decimales periódicos simples, que son aquellos en los que se repite un solo dígito después del punto decimal. Estos se llaman "números decimales periódicos simples de período 1". Por ejemplo, el número 0.333... se llama "treintatresésimo".
Luego, tenemos los números decimales periódicos mixtos, que son aquellos en los que se repiten más de un dígito después del punto decimal. A este tipo de números se les asigna un nombre especial que indica los dígitos que se repiten. Por ejemplo, el número 0.1616... se llama "dieciséis-veinticinco milésimos".
Es importante distinguir entre los números decimales periódicos finitos y los periódicos puros. Los números decimales periódicos finitos son aquellos que tienen una secuencia finita de dígitos después del punto decimal que se repite. A estos números se les agrega el sufijo "-avo" para indicar la repetición. Por ejemplo, el número 0.1313 se llama "trece-e trece-avos". Por otro lado, los números decimales periódicos puros son aquellos en los que la secuencia repetitiva incluye todos los dígitos después del punto decimal. A estos números se les agrega el sufijo "-oide" para indicar la repetición completa. Por ejemplo, el número 0.777... se llama "setenta-y-siete-oideos".
Ahora que conoces cómo representar y nombrar los números decimales periódicos, podrás comprender plenamente su significado y utilizarlos correctamente en situaciones matemáticas y de la vida cotidiana.
Qué es un número decimal no periódico
Un número decimal no periódico es un tipo de número que se obtiene al dividir dos números enteros y el resultado es un cociente con una parte entera seguida de una parte decimal infinita y no repetitiva. Esto significa que la secuencia de dígitos después del punto decimal nunca se repite en un patrón fijo.
Estos números son fascinantes porque a primera vista pueden parecer caóticos, pero en realidad tienen una estructura matemática muy interesante. Cada dígito después del punto decimal tiene un valor específico y cada uno de ellos cuenta algo importante sobre el número en sí.
Cómo se leen los números decimales no periódicos
Para leer los números decimales no periódicos correctamente, es necesario entender cómo se agrupan los dígitos y asignarles un nombre según su posición. Es similar a cómo funcionan los números enteros, pero con algunos cambios sutiles debido a la presencia de la parte decimal.
A continuación, te proporcionaré una lista con los nombres correspondientes a cada dígito que puede aparecer en un número decimal no periódico:
- 0: cero
- 1: uno
- 2: dos
- 3: tres
- 4: cuatro
- 5: cinco
- 6: seis
- 7: siete
- 8: ocho
- 9: nueve
Además de estos dígitos individuales, los números decimales no periódicos también pueden tener algunas secuencias especiales que se leen de una manera distinta. Aquí tienes algunas de las más comunes:
- 10: diez
- 11: once
- 20: veinte
- 21: veintiuno
- 100: cien
- 101: ciento uno
- 1000: mil
- 1001: mil uno
Estas secuencias son importantes porque se utilizan en muchas situaciones cotidianas donde se necesita expresar cantidades precisas con números decimales.
El significado detrás de cada posición
En un número decimal no periódico, cada posición después del punto decimal tiene un valor específico y representa una fracción diferenciada del número total. Estas posiciones se agrupan en potencias de diez, al igual que en los números enteros.
Aquí tienes una tabla que muestra el valor de cada posición en un número decimal no periódico:
| Posición | Valor |
|---|---|
| 1 | Décimos |
| 2 | Centésimos |
| 3 | Milésimos |
| 4 | Diezmilésimos |
| 5 | Cienmilésimos |
| 6 | Millonésimos |
| 7 | Diezmillonésimos |
| 8 | Cienmillonésimos |
| 9 | Milmillonésimos |
| 10 | Diezmilmillonésimos |
Estos son solo algunos ejemplos de las posiciones y los nombres que se les atribuyen en un número decimal no periódico. Dependiendo del número en sí, la parte decimal puede ser mucho más larga y tener una variedad de dígitos y valores.
Conocer el significado detrás de cada posición es fundamental para comprender mejor el valor numérico que representa un número decimal no periódico y para poder utilizarlo en diferentes contextos.
Puedes dar ejemplos de números decimales no periódicos
Los números decimales no periódicos son aquellos que tienen una secuencia de dígitos que no se repite de forma regular o periódica. A diferencia de los números decimales periódicos, en los que la misma secuencia de dígitos se repite infinitamente, los decimales no periódicos presentan una secuencia única y no repetitiva.
Para comprender mejor estos números, es útil dar algunos ejemplos. Uno de los más conocidos es el número π (pi), cuya representación decimal no tiene un patrón recurrente. Los dígitos de π se extienden hasta el infinito sin repetirse de manera periódica.
Otro ejemplo es el número e, también llamado la base del logaritmo natural. La representación decimal de e tampoco sigue un patrón regular y sus dígitos se prolongan infinitamente sin repetirse periódicamente.
El número √2 (raíz cuadrada de 2) también es un ejemplo de número decimal no periódico. La representación decimal de √2 tiene una secuencia infinita de dígitos que no se repite periódicamente.
Además de estos ejemplos famosos, existen numerosos números decimales no periódicos que pueden surgir en diferentes contextos matemáticos y científicos. Algunos de ellos tienen aplicaciones prácticas en campos como la física, la criptografía y la teoría de números.
Los números decimales no periódicos son aquellos que no siguen un patrón recurrente en su representación decimal. Estos números, como π, e y √2, presentan una secuencia única y no repetitiva de dígitos que se extiende infinitamente.
Cuál es la diferencia entre una fracción decimal y un número decimal
Antes de sumergirnos en los nombres de los números después del punto decimal, es importante entender la diferencia entre una fracción decimal y un número decimal. Ambos conceptos están relacionados con la representación de valores numéricos que no son enteros, pero se utilizan en contextos diferentes.
Una fracción decimal se refiere a una fracción cuyo denominador es una potencia de diez (10, 100, 1000, etc.). Esto significa que el número se puede expresar como una división donde el denominador es un múltiplo de 10. Por ejemplo, 0.5 es una fracción decimal porque se puede escribir como 5/10 o como 1/2.
Por otro lado, un número decimal es cualquier número que incluya una parte fraccionaria después del punto decimal. Estos números pueden ser periódicos o no periódicos. Un número decimal periódico es aquel en el que una secuencia de dígitos se repite infinitamente, como 0.3333..., mientras que un número decimal no periódico no sigue ningún patrón repetitivo, como pi (π) o raíz cuadrada de 2 (√2).
La principal diferencia entre una fracción decimal y un número decimal radica en su forma de expresión matemática. Mientras que las fracciones decimales se escriben utilizando la notación de fracciones, los números decimales se representan directamente con la parte entera seguida de la parte fraccionaria separada por un punto decimal.
Es importante tener en cuenta que los números decimales también se pueden expresar como fracciones decimales si se desea. Por ejemplo, 0.75 se puede escribir como 75/100 o reducido como 3/4. Sin embargo, no todos los números decimales tienen una representación exacta como fracción decimal, ya que algunos pueden ser irracionales y no se pueden expresar de manera finita o periódica.
La diferencia fundamental entre una fracción decimal y un número decimal radica en su forma de expresión y en qué tipo de valores numéricos representan. Las fracciones decimales son aquellos que se pueden expresar como divisiones con múltiplos de diez como denominadores, mientras que los números decimales incluyen cualquier número con una parte fraccionaria después del punto decimal, ya sea periódica o no periódica.
Cuáles son los nombres de los primeros números decimales
Cuando nos encontramos trabajando con números decimales, es importante conocer los nombres de los números que se encuentran después del punto decimal. Estos nombres nos permiten referirnos a cada uno de estos valores y entender su posición en el número decimal.
El primer número decimal después del punto se llama décima. Este es el número que está a una posición después del punto decimal, y se representa con el símbolo 0.1. La décima parte de un número es una fracción que tiene un denominador de 10.
A continuación, tenemos la centésima. Esta es la segunda posición después del punto decimal y se representa como 0.01. La centésima parte de un número es una fracción con un denominador de 100.
En tercer lugar, encontramos la milésima. Este número se ubica tres posiciones después del punto decimal y su representación es 0.001. La milésima parte de un número corresponde a una fracción con un denominador de 1000.
Luego, nos encontramos con la diezmilésima. Este número ocupa la cuarta posición después del punto decimal y se denota como 0.0001. La diezmilésima parte de un número se obtiene mediante una fracción con un denominador de 10000.
Después de la diezmilésima, sigue la cienmilésima. Este número se encuentra en la quinta posición después del punto decimal y se representa con el valor 0.00001. La cienmilésima parte de un número se obtiene a partir de una fracción cuyo denominador es 100000.
La siguiente posición después del punto decimal es la millonésima. Representada como 0.000001, la millonésima es la sexta posición decimal. La millonésima parte de un número se obtiene mediante una fracción con denominador 1000000.
Continuando con los nombres de los números decimales, encontramos la diezmillonésima. Este número se ubica en la séptima posición después del punto decimal y se representa como 0.0000001. La diezmillonésima parte de un número se obtiene utilizando una fracción con denominador de 10000000.
Después de la diezmillonésima, seguimos con la cienmillonésima. Este número se encuentra en la octava posición después del punto decimal y se denota como 0.00000001. La cienmillonésima parte de un número se obtiene mediante una fracción con denominador 100000000.
En la siguiente posición decimal, tenemos la milmillonésima. Representada como 0.000000001, la milmillonésima es la novena posición decimal. La milmillonésima parte de un número corresponde a una fracción con un denominador de 1000000000.
Finalmente, en la décima posición decimal después del punto nos encontramos con la diezmilmillonésima. Esta fracción se representa como 0.0000000001. La diezmilmillonésima parte de un número se obtiene mediante una fracción cuyo denominador es 10000000000.
Es importante conocer estos nombres y su significado al trabajar con números decimales. Nos permiten expresarlos de forma más precisa y entender su relación con otros números dentro del sistema decimal.
Preguntas frecuentes (FAQ)
1. ¿Cuáles son los nombres de los números después del punto decimal?
Los nombres de los números después del punto decimal son: décimas, centésimas, milésimas, diezmilésimas y así sucesivamente.
2. ¿Qué significa decir que un número tiene tres decimales?
Decir que un número tiene tres decimales significa que hay tres dígitos después del punto decimal.
3. ¿Cómo se leen los números después del punto decimal en español?
Los números después del punto decimal se leen de la siguiente manera: 0.1 se lee "cero enteros uno décima", 0.25 se lee "cero enteros veinticinco centésimas".
4. ¿Cuál es el valor posicional de los números después del punto decimal?
El valor posicional de los números después del punto decimal disminuye en potencias de diez: décimas (10^-1), centésimas (10^-2), milésimas (10^-3), etc.
5. ¿Puede haber números negativos después del punto decimal?
Sí, puede haber números negativos después del punto decimal. Por ejemplo, -0.5 sería "menos cero enteros cinco décimas".

Deja una respuesta